Σημειωματάριο Τρίτης, 17 Μαρ. 2015
Γραφήματα
Ένα γράφημα αποτελείται από ένα σύνολο κορυφών ή κόμβων. Κάποια ζεύγη κορυφών μπορούν να συνδέονται μεταξύ τους με ακμές.
Ως παράδειγμα γραφήματος με το οποίο θα ασχοληθούμε σήμερα μπορείτε να δείτε το παρακάτω όπου ως κορυφές έχουμε τα ονόματα κάποιων ατόμων. Έχουμε ακμή από μια κορυφή σε μια άλλη αν τα δύο αυτά άτομα είναι μεταξύ τους φίλοι. Έτσι, για παράδειγμα, στο παρακάτω γράφημα ο Μανώλης με το Γιάννη είναι μεταξύ τους φίλοι ενώ ο Δημήτρης δεν είναι φίλος με την Κατερίνα.
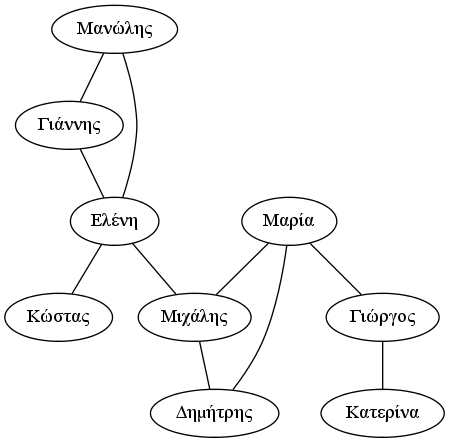
Το γράφημα αυτό το έχουμε περιγράψει στο αρχείο graph.txt το οποίο θα πρέπει να κατεβάσετε στον υπολογιστή σας για να τρέξει το πρόγραμμα που υπάρχει παρακάτω. Στο αρχείο αυτό έχουμε περιγράψει, μία σε κάθε γραμμή, όλες τις ακμές του γραφήματος.
Οι λίστες των φίλων του κάθε ατόμου (γείτονες κάθε κορυφής)
Στις πρώτες γραμμές του παρακάτω προγράμματος
f = open("graph.txt", "r")
lines = f.readlines()
f.close()ανοίγουμε και διαβάζουμε το αρχείο αυτό. Επόμενο μέλημά μας είναι να δημιουργήσουμε για κάθε μια κορυφή (δηλ. για κάθε άτομο) τη λίστα όλων των φίλων του, τη λίστα δηλ. όλων των κορυφών του γραφήματος με τις οποίες συνδέεται με ακμή (αυτές ονομάζονται οι γειτονικές του κορυφές).
Γι' αυτό δημιουργούμε ένα λεξικό g, αρχικά κενό, όπου για κάθε κορυφή (για κάθε όνομα) θα υπολογίζουμε μια λίστα, τη λίστα των φίλων του. Για να το κάνουμε αυτό διανύουμε τις γραμμές του αρχείου εισόδου (που τις έχουμε αποθηκεύσει στη λίστα lines) και, κατ' αρχήν, διαβάζουμε μέσα από το κάθε string της λίστας αυτής τα δύο ονόματα που εμφανίζονται στη λίστα names με την εντολή
names = l.rstrip().split(" ")η οποία αφού πρώτα απαλείψει από το τέλος του string l τους λευκούς χαρακτήρες (συμπεριλαμβανομένου του newline) με τη μέθοδο rstrip και από αυτό το string παίρνουμε τη λίστα names που περιέχει μέσα δύο strings, αυτά που προκύπτουν αν θεωρήσουμε τον κενό χαρακτήρα " " ως διαχωριστικό (αυτό κάνει η μέθοδος split(" ")). Τα δύο αυτά ονόματα τα κρατάμε έπειτα στις μεταβλητές a, b για ευκολία μας. Αυτό που πρέπει τώρα να γίνει, και το οποίο επιτυγχάνεται με τη συνάρτηση fix που είναι γραμμένη πιο πάνω, είναι ότι πρέπει να προσθέσουμε το b στους φίλους του a (αν δεν είναι ήδη μέσα) και επίσης να προσθέσουμε το a στους φίλους του b. Αυτή ακριβώς είναι η δουλειά της συνάρτησης
def fix(x, y, di):
"Ταχτοποιεί τον y ως γείτονα του x στο λεξικό di"
if x in di:
if not(y in di[x]):
di[x].append(y)
else:
di[x] = [y]Η συνάρτηση fix ελέγχει αν ο y είναι ήδη ανάμεσα στους γείτονες (φίλους) του x και, αν δεν είναι, τον βάζει.
Έπειτα τυπώνουμε όλα τα άτομα και τους φίλους του καθενός σε μια γραμμή δίπλα του.
Οι αποστάσεις όλων των κορυφών από την κορυφή "Γιάννης"
Το επόμενό μας μέλημα είναι να υπολογίσουμε την απόσταση όλων των κορυφών από μια συγκεκριμένη κορυφή, την κορυφή "Γιάννης". Απόσταση ανάμεσα σε δύο κορυφές ενός γραφήματος είναι το ελάχιστο πλήθος ακμών που πρέπει κανείς να διανύσει για να πάει από τη μια κορυφή στην άλλη. Για παράδειγμα, η απόσταση του Γιάννη από τον εαυτό του είναι 0 ενώ η απόσταση του Μανώλη και της Ελένης από το Γιάννη είναι 1. Θα πρέπει λοιπόν να υπολογίσουμε αυτό τον αριθμό για κάθε μια κορυφή του γραφήματος.
Την απόσταση αυτή την κρατάμε στο λεξικό dist και κατ' αρχήν βάζουμε στο κάθε άτομο τιμή ίση με -1, που είναι ο τρόπος που χρησιμοποιούμε για να δηλώσουμε ότι η τιμή δεν έχει υπολογιστεί ακόμη.
Η στρατηγική μας για τον υπολογισμό των αποστάσεων από την κορυφή "Γιάννης" (στην οποία αναφερόμαστε με τη μεταβλητή s) είναι η εξής. Κατ' αρχήν βάζουμε την dist[s] = 0 και ορίζουμε τη λίστα justnumbered να περιέχει μόνο την κορυφή s. Το νόημα που αποδίδουμε στη μεταβλητή justnumbered είναι ότι θα αντιπροσωπεύει το ποιες κορυφές είναι αυτές που η απόστασή τους από το s προσδιορίστηκε ακριβώς στο προηγούμενο βήμα της ανακύκλωσης. Φανταστείτε ότι από την κορυφή s ξεκινάει να μεταδίδεται ένα "κύμα". Σε κάθε χρονική στιγμή το κύμα αυτό διανύει μόνο μια ακμή. Στη χρονική στιγμή 0 το κύμα αυτό βρίσκεται περιορισμένο στην αρχική κορυφή s. Τη χρονική στιγμή 1 το κύμα αυτό έχει μεταφερθεί στους άμεσους γείτονες των κορυφών στις οποίες βρισκόταν πριν, δηλ. στις κορυφές "Μανώλης" και "Ελένη". Αυτές οι δύο κορυφές πρέπει συνεπώς να πάρουν αριθμό (απόσταση από την s) ίση με 1. Την επόμενη χρονική στιγμή παίρνουμε το κύμα από τις δύο αυτές κορυφές στις οποίες έχει φτάσει και το προχωράμε ακόμη κατά μία ακμή. Έτσι φτάνει στις δύο νέες κορυφές "Κώστας" και "Μιχάλης". Αυτές οι κορυφές θα πάρουν αριθμό 2 αφού το κύμα χρειάστηκε δύο χρονικές μονάδες γαι να φτάσει εκεί. Τη χρονική στιγμή 3 το κύμα θα φτάσει στις δύο κορυφές "Μαρία" και "Δημήτρης" και αυτές θα πάρουν απόσταση 3 από το s. Τη χρονική στιγμή 4 το κύμα θα φτάσει στο Γιώργο και τη χρονική στιγμή 4 θα φτάσει στην Κατερίνα. Από κει και πέρα σταματάσει να μεταδίδεται γιατι όλες οι κορυφές έχουν ηδη πάρει απόσταση.
Σε κάθε εκτέλεση της ανακύκλωσης while κοιτάμε όλες τις κορυφές που είναι στη λίστα justnumbered και που είναι οι κορυφές που πήραν απόσταση από το s στην προηγούμενη εκτέλεση της ανακύκλωσης. Στη λίστα tobenumbered βάζουμε όλους τους φίλους των μελών της justnumbered που (α) δεν έχουν αριθμηθεί ακόμη (και άρα έχουμε το dist τους ακόμη ίσο με -1) και (β) δεν έχουν ήδη τοποθετηθεί στη λίστα tobenumbered (γιατί δε θέλουμε να τους βάλουμε δύο φορές, για λόγους αποτελεσματικότητας της εκτέλεσης του προγράμματος). Αφού βρούμε ποια είναι η λίστα tobenumbered βάζουμε σε όλες αυτές τις κορυφές απόσταση ίση με την προηγούμενη απόσταση (μεταβλητή distance) συν 1 και αυξάνουμε κατά 1 τη μεταβλητή αυτή. Τέλος αντιγράφουμε τη λίστα tobenumbered στη λίστα justnumbered. Η ανακύκλωση while θα σταματήσει όταν η λίστα justnumbered καταστεί κενή, όταν δηλ. το "κύμα" έχει σταματήσει να προχωράει.
Τέλος τυπώνουμε για κάθε κορυφή την απόστασή της από την κορυφή "Γιάννης".
Εύρεση όλων των τριγώνων στο γράφημα.
Στο υπόλοιπο του προγράμματος βρίσκουμε τα τρίγωνα του γραφήματος. Ένα σύνολο τριών κορυφών σ' ένα γράφημα λέγεται τρίγωνο αν και οι τρεις κορυφές είναι μεταξύ τους γειτονικές.
Εδώ θα χρησιμοποιήσουμε για πρώτη φορά ένα σύνολο (set) που είναι κάτι σα μια λίστα αλλά με τις εξής διαφορές: (α) ένα στοιχείο δε μπορεί να συμμετέχει στο σύνολο παραπάνω από μια φορά, (β) τα σύνολα δεν έχουν εσωτερική διάταξη όπως έχουν οι λίστες (και σε αυτό τα σύνολα μοιάζουν με τα λεξικά).
Αν έχουμε δύο λίστες λίστα
l1 = [1, 2, 2, 3]
l2 = [3, 2, 2, 2, 1, 1]οι οποίες περιέχουν τα ίδια στοιχεία αν δε λάβουμε υπόψιν μας τη σειρά με την οποία εμφανίζονται και το πόσες (παραπάνω από μία) φορές εμφανίζονται, τότε μπορούμε από κάθε μια τέτοια λίστα να φτιάξουμε το αντίστοιχο σύνολο με τη συάρτηση set
s1 = set(l1)
s2 = set(l2)
print s1
print s2
if s1 == s2:
print "Τα σύνολα είναι ίδια."το output που παίρνουμε είναι
set([1, 2, 3])
set([1, 2, 3])
Τα σύνολα είναι ίδια.και παρατηρείστε ότι αυτές οι δύο λίστες l1 και l2 δίδουν τελικά τα ίδια σύνολα (το αναμενόμενο). Αν θέλουμε λοιπόν να συγκρίνουμε μεταξύ τους δύο λίστες και θέλουμε να θεωρηθούν ίδιες αν περιέχουν τα ίδια στοιχεία, ανεξαρτήτως σειράς ή πολλαπλότητας εμφάνισης, τότε μπορούμε να συγκρίνουμε τα σύνολα που προκύπτουν από τις δύο λίστες.
Για να βρούμε λοιπόν όλα τα τρίγωνα του γραφήματος κατ' αρχήν διανύουμε με τη μεταβλητή x όλα τα όνοματα (κορυφές του γραφήματος) και για κάθε κορυφή x που επισκεπτόμαστε διανύουμε τη λίστα των γειτόνων του x ανεξάρτητα με τις δύο μεταβλητές y και z. Αν για δύο τέτοιες κορυφές y και z διαπιστώσουμε ότι είναι και μεταξύ τους γειτονικές τότε έχουμε βρει το τρίγωνο με κορυφές x, y και z. Αυτό το τρίγωνο το βάζουμε στη λίστα triangles (αρχικά κενή) αν δεν είναι ήδη μέσα, αλλά επειδή δε θέλουμε να λάβουμε υπόψιν μας τη σειρά των κορυφών x, y και z αντί να βάλουμε τη λίστα [x, y, z] στη λίστα triangles βάζουμε το σύνολο set([x, y, z]) που προκύπτει από αυτή τη λίστα. Έτσι η λίστα triangles περιέχει σύνολα με τρία στοιχεία το καθένα και όχι λίστες.
Στο τέλος του προγράμματος τυπώνουμε όλα τα τρίγωναπου βρήκαμε.