


Next: 5.38 Δεσμευμένη πυκνότητα δύο
Up: 5 Ημερολόγιο διαλέξεων
Previous: 5.36 Ένατη ομάδα ασκήσεων
Contents
Κατ' αναλογία με τη διακριτή περίπτωση ορίσαμε τη συνέλιξη δύο
συναρτήσεων
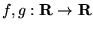 , που πληρούν
, που πληρούν
ως τη συνάρτηση
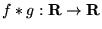 που ορίζεται από
που ορίζεται από
Είδαμε διάφορες ιδιότητες της συνέλιξης, όλες τους ανάλογες
αυτών της διακριτής περίπτωσης, και δείξαμε τέλος ότι αν
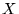 και
και 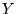 είναι δύο ανεξάρτητες ΤΜ με πυκνότητες τότε
η πυκνότητα της
είναι δύο ανεξάρτητες ΤΜ με πυκνότητες τότε
η πυκνότητα της 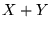 δίδεται από τον τύπο
δίδεται από τον τύπο
Υπολογίσαμε διάφορα παραδείγματα από το βιβλίο.
Mihalis Kolountzakis
![]() , που πληρούν
, που πληρούν