Σημειωματάριο Τετάρτης 29 Νοε. 2017¶
Γραφήματα (γράφοι), η αναπαράστασή τους στον υπολογιστή και μερικά προβλήματα σε αυτά¶
Είδαμε σήμερα λίγα πράγματα για γραφήματα (ή γράφους). Γράφημα είναι, στην απλούστερή του μορφή, ένα σύνολο $V$ από κορυφές (ή κόμβους) και ένα σύνολο $E$ από ακμές (μια ακμή είναι ένα ζεύγος κόμβων, στην απλούστερη περίπτωση μη διατεταγμένο). Συνιστώ να ρίξετε μια ματιά στο Κεφ. 5 του βιβλίου
"Διακριτά Μαθηματικά" (Μ. Κολουντζάκης, Χρ. Παπαχριστόδουλος)
όπου θα δείτε αρκετά παραδείγματα στις πρώτες σελίδες του Κεφαλαίου.
Πώς αναπαριστούμε στον υπολογιστή την πληροφορία των κορυφών και των συνδέσεών (ακμών) τους;
Ο πρώτος τρόπος είναι να αραδιάσουμε όλες τις κορυφές σε μια λίστα, ας την πούμε V, και όλες τις ακμές (ζεύγη κορυφών, δηλ. στοιχείων της λίστας V) σε μια λίστα, ας την πούμε E.
Για το παρακάτω γράφημα, για παράδειγμα,
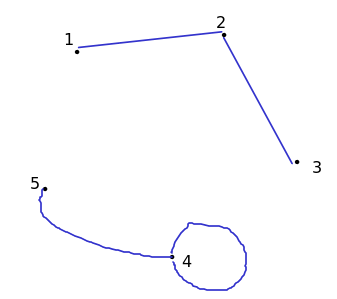
έχουμε τις λίστες
V = [1, 2, 3, 4, 5]
E = [ [2, 1], [2, 3], [4, 4], [4, 5] ]
ως αναπαράστασή του.
Ένας δεύτερος τρόπος αναπαράστασης του γραφήματος στον υπολογιστή είναι κάπως πιο "κορυφοκεντρικός". Κρατάμε δηλ. για κάθε κορυφή του γραφήματος τη λίστα των γειτόνων του, των κορυφών δηλ. που συνδέονται με αυτήν με κάποια ακμή. Ο φυσιολογικός τρόπος να κρατήσουμε αυτήν την πληροφορία είναι σε ένα λεξικό που έχει ως κλειδιά της κορυφές και ως τιμή κάθε κλειδιού τη λίστα των γειτόνων του. Για το παραπάνω γράφημα έχουμε το λεξικό:
Neighbor = {
1: [2],
2: [1, 3],
3: [2],
4: [4, 5],
5: [4]
}
Η πρώτη μας δουλειά είναι να υπολογίσουμε τη δεύτερη αναράσταση του γραφήματος από την πρώτη και το αντίστροφο.
V = [1, 2, 3, 4, 5]
E = [ [2, 1], [2, 3], [4, 4], [4, 5] ]
Neighbor = {} # αυτό είναι το λεξικό που θα φτιάξουμε από τα V, E παραπάνω
for v in V: # εισάγουμε κατ' αρχήν όλα τα κλειδιά του λεξικού (όλες τις κορυφές) χωρίς κανένα γείτονα
Neighbor[v] = []
for e in E: # για κάθε ακμή e στο E
a = e[0] # έστω a, b οι δύο κορυφές της ακμής
b = e[1]
if a == b: # οι δύο κορυφές μπορεί και να συμπίπτουν
Neighbor[a].append(a) # σε αυτή την περίπτωση κάνουμε μόνο μια προσθήκη, στην κορυφή a
else: # αν οι κορυφές είναι διαφορετικές
Neighbor[a].append(b) # βάζουμε την b στη λίστα γειτόνων της a
Neighbor[b].append(a) # και την a στη λίστα γειτόνων της b
print(Neighbor)
Τώρα ξεκινάμε από τη δεύτερη αναπαράσταση (λεξικό Neighbor) και κατασκευάζουμε την πρώτη (λίστες E, V).
Neighbor = {1: [2], 2: [1, 3], 3: [2], 4: [4, 5], 5: [4]}
V = list(Neighbor.keys()) # οι κορυφές είναι τα κλειδιά του λεξικού
E = [] # η λίστα ακμών είναι κατ' αρχήν κενή
for v in V: # για κάθε κορυφή v
V1 = Neighbor[v] # ας είναι V1 η λίστα των γειτόνων του
for w in V1: # για κάθε γείτονα w του v
if [w, v] in E: # υπάρχει περίπτωση να έχει ήδη μπει η ακμή στο E με πρώτη κορυφή την w
continue # σε αυτή την περίπτωση δεν κάνουμε τίποτα
E.append([v, w]) # αν δεν υπάρχει η ακμή τη βάζουμε στο E
print("V =", V)
print("E =", E)
Η συνεκτική συνιστώσα μιας κορυφής $v$ ενός γραφήματος είναι το σύνολο όλων των κορυφών του γραφήματος που είναι προσβάσιμες από την $v$, στις οποίες δηλ. μπορούμε να πάμε ξεκινώντας από την $v$ και κινούμενοι πάνω στις υπάρχουσες ακμές του γραφήματος. Οι κορυφές του γραφήματος χωρίζονται έτσι σε (ξένες μεταξύ τους) συνεκτικές συνιστώσες.
Δύο κορυφές $a$ και $b$ είναι προσβάσιμες η μια από την άλλη (μιλάμε πάντα για ακμές χωρίς κατεύθυνση) αν και μόνο αν ανήκουν στην ίδια συνεκτική συνιστώσα του γραφήματος.
Για παράδειγμα στο γράφημα
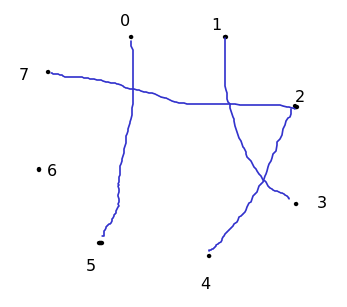
οι συνεκτικές συνιστώσες είναι οι $$ \{0, 5\},\ \{1, 3\},\ \{2, 4, 7\},\ \{6\}. $$
Στο παρακάτω πρόγραμμα υπολογίζουμε με τη συνάρτηση component τη συνιστώσα της κορυφής v στο γράφημα του οποία η συνδεσμολογία περιγράφεται στο λεξικό N.
Neighbor = {
0: [5], 1: [3], 2: [4, 7], 3: [1],
4: [2], 5: [0], 6: [], 7: [2],
}
def component(N, v):
# Επιστρέφει σε μια λίστα όλες τις κορυφές
# της συνεκτικής συνιστώσας του v
L = [ v ] # κατ' αρχήν μόνο το v ανήκει στη συνιστώσα του
while True: # συνεχώς κοιτάμε τους γείτονες της συνιστώσας (λίστα L) μέχρι στιγμής
# για να ανακαλύψουμε κι άλλες κορυφές της συνιστώσας (τις βάζουμε στη λίστα wave)
wave = [] # θα είναι οι νέοι γείτονες του L
for w in L: # για κάθε κορυφή w της λίστας L
for x in N[w]: # και για κάθε γείτονα x της w
if (x not in L) and (x not in wave): # αν η x δεν είναι ήδη στο wave ή στο L
wave.append(x) # βάζουμε την x στο wave
L = L+wave # επαυξάνουμε τη λίστα (συνεκτική συνιστώσα) με τις κορυφές της λίστας wave
if wave==[]: # αν το wave ήταν κενό (δεν ανακαλύψαμε κανένα καινούργιο στοιχείο) σταματάμε το loop
break
return L # επιστρέφουμε τη συνεκτική συνιστώσα
# τα παρακάτω επιστρέφουν διαφορετικές λίστες αλλά με τα ίδια στοιχεία, μια και το 4 είναι προσβάσιμο από το 7
print(component(Neighbor, 4))
print(component(Neighbor, 7))
Στο παρακάτω χρησιμοποιούμε την component για να βρούμε με τη συνάρτηση allcomponents όλες τις συνεκτικές συνιστώσες ενός γραφήματος.
Neighbor = {
0: [5], 1: [3], 2: [4, 7], 3: [1],
4: [2], 5: [0], 6: [], 7: [2],
}
def component(N, v):
# Επιστρέφει σε μια λίστα όλες τις κορυφές
# της συνεκτικής συνιστώσας του v
L = [ v ] # κατ' αρχήν μόνο το v ανήκει στη συνιστώσα του
while True: # συνεχώς κοιτάμε τους γείτονες της συνιστώσας (λίστα L) μέχρι στιγμής
# για να ανακαλύψουμε κι άλλες κορυφές της συνιστώσας (τις βάζουμε στη λίστα wave)
wave = [] # θα είναι οι νέοι γείτονες του L
for w in L: # για κάθε κορυφή w της λίστας L
for x in N[w]: # και για κάθε γείτονα x της w
if (x not in L) and (x not in wave): # αν η x δεν είναι ήδη στο wave ή στο L
wave.append(x) # βάζουμε την x στο wave
L = L+wave # επαυξάνουμε τη λίστα (συνεκτική συνιστώσα) με τις κορυφές της λίστας wave
if wave==[]: # αν το wave ήταν κενό (δεν ανακαλύψαμε κανένα καινούργιο στοιχείο) σταματάμε το loop
break
return L # επιστρέφουμε τη συνεκτική συνιστώσα
def allcomponents(N):
# επιστρέφει μια λίστα με όλες τις συνεκτικές συνιστώσες του γραφήματος N
V = list(N.keys()) # αυτές είναι οι κορυφές
Components = [] # η λίστα που επιστρέφουμε, αρχικά κενή
while True: # βρίσκουμε συνεχώς συνεκτικές συνιστώσες
# για κάθε μια που βρίσκουμε αφαιρούμε τις κορυφές της από το V έως ότου αυτό μείνει κενό.
v = V[0] # η πρώτη κορυφή (που έχει απομείνει στο V)
L = component(N, v) # η L είναι η συνεκτική συνιστώσα του v
Components.append(L) # προσθέτουμε τη συνιστώσα L στο αποτέλεσμα που θα επιστρέψουμε
for w in L: # για κάθε κορυφή w της συνιστώσας L
V.remove(w) # την αφαιρούμε από το σύνολο κορυφών
if V==[]: # αν το σύνολο κορυφών έχει μείνει κενό τελειώσαμε
break
return Components # επιστρέφουμε τη λίστα με τις συνιστώσες
print(allcomponents(Neighbor))
Στο παρακάτω γράφημα
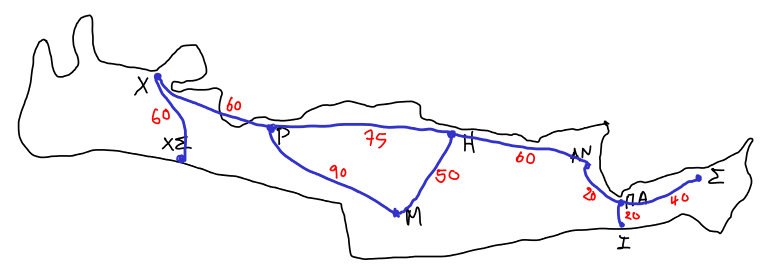
με κορυφές κάποιες πόλεις της Κρήτης οι διάφορες ακμές έχουν μια επιπλέον πληροφορία που τις συνοδεύει, ένα πραγματικό (θετικό) αριθμό, το μήκος τους.
Για να παραστήσουμε ένα τέτοιο γράφημα στον υπολογιστή θα πρέπει για κάθε ακμή να κρατάμε κι ένα αριθμό μαζί. Αυτό βολεύει να το κάνουμε κρατώντας τους γείτονες μιας κορυφής όχι απλά σε μια λίστα αλλά σε ένα λεξικό με κλειδί τις κορυφές και τιμές τις αποστάσεις από την κορυφή. Έτσι το παρακάτω γράφημα το αναπαριστούμε με το λεξικό
Graph = {
'ΧΣ': {'Χ': 60},
'Χ': {'ΧΣ': 60, 'Ρ': 60},
'Ρ': {'Χ': 60, 'Μ': 90, 'Η': 75},
'Μ': {'Ρ': 90, 'Η': 50},
'Η': {'Ρ': 75, 'Μ': 50, 'ΑΝ': 60},
'ΑΝ': {'Η': 60, 'ΠΑ': 20},
'ΠΑ': {'ΑΝ': 20, 'Ι': 20, 'Σ': 40},
'Ι': {'ΠΑ': 20},
'Σ': {'ΠΑ': 40},
}
Την επόμενη φορά θα δούμε πώς θα λύσουμε το βασικό πρόβλημα της εύρεσης αποστάσεων σε ένα τέτοιο γράφημα.