Σημειωματάριο Δευτέρας 4 Δεκ. 2017¶
Ο αλγόριθμος Floyd-Warshall για την έυρεση όλων των αποστάσεων σε ένα γράφημα με βάρη στις ακμές¶
Συνεχίσαμε σήμερα το θέμα της προηγούμενης Τετάρτης. Έχουμε ένα γράφημα στο οποίο οι ακμές έχουν κάποια βάρη επάνω τους (κάποιους μη αρνητικούς αριθμούς). Στο παράδειγμά μας έχουμε ένα γράφημα όπου κορυφές είναι κάποιες πόλεις της Κρήτης και τα βάρη πάνω σε ένα δρόμο (ακμή) από πόλη σε πόλη παριστάνουν την απόσταση σε χιλιόμετρα.
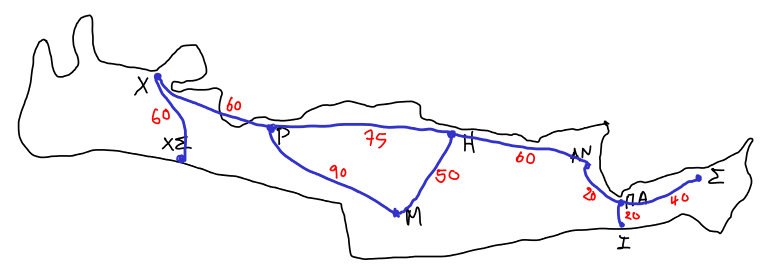
Το γράφημα αυτό αναπαριστάμε όπως φαίνεται παρακάτω, σε ένα λεξικό όπου κλειδιά είναι οι πόλεις και η τιμή κάθε πόλης είναι επίσης ένα λεξικό. Στο λεξικό της κάθε πόλης κλειδιά είναι μόνο οι πόλεις που συνδέονται με αυτήν και τιμές αυτών είναι οι αποστάσεις τους.
Graph = {
'ΧΣ': {'Χ': 60},
'Χ': {'ΧΣ': 60, 'Ρ': 60},
'Ρ': {'Χ': 60, 'Μ': 90, 'Η': 75},
'Μ': {'Ρ': 90, 'Η': 50},
'Η': {'Ρ': 75, 'Μ': 50, 'ΑΝ': 60},
'ΑΝ': {'Η': 60, 'ΠΑ': 20},
'ΠΑ': {'ΑΝ': 20, 'Ι': 20, 'Σ': 40},
'Ι': {'ΠΑ': 20},
'Σ': {'ΠΑ': 40},
}
Σκοπός μας είναι να βρούμε την απόσταση κάθε πόλης του γραφήματος από κάθε άλλη. Η απόσταση ανάμεσα σε δύο πόλεις είναι, εξ' ορισμού, το ελάχιστο μήκος μονοπατιού ξεκινά από τη μια πόλη και καταλήγει στην άλλη.
Το να προσπαθήσει κανείς να βρει την απόσταση ανάμεσα σε δύο πόλεις ελέγχοντας όλα τα μονοπάτια που πάνε από τη μια στην άλλη μπορεί να είναι εξαιρετικά χρονοβόρο μια και μπορεί να υπάρχουν πάρα πολλοί τρόποι να κινηθεί κανείς ώστε να πάει από τη μια πόλη στην άλλη. Είναι φανερό λοιπόν ότι χρειαζόμαστε κάποιον ειδικό αλγόριθμο για αυτό το πρόβλημα. Ο αλγόριθμος που θα δούμε εδώ λέγεται αλγόριθμος Floyd-Warshall.
Εδώ θα περιγράψουμε ένα αλγόριθμο που βρίσκει όλες τις αποστάσεις ανάμεσα σε όλα τα ζευγάρια κορυφών, σε ένα γράφημα $G$ με (μη αρνητικά) βάρη στις ακμές του. Πρέπει να τονίσουμε ότι το πρόβλημα που λύνουμε εδώ αλγοριθμικά είναι το πρόβλημα των αποστάσεων από <<οποιαδήποτε σε οποιαδήποτε>> κορυφή. Στο τέλος του αλγορίθμου δηλ.\ θα μπορούμε να απαντήσουμε άμεσα (σε σταθερό χρόνο, όπως λέμε) σε κάθε ερώτημα <<ποια είναι η απόσταση ανάμεσα στις κορυφές $i$ και $j$ του γραφήματος;>>.
Αν δε μας ενδιέφερε αυτή η γενικότητα αλλά θέλαμε, π.χ., να γνωρίζουμε, μετά το
πέρας του αλγορίθμου, όλες τις αποστάσεις από την κορυφή $1$ προς όλες τις άλλες,
τότε θα χρησιμοποιούσαμε διαφορετικό αλγόριθμο.
Ο αλγόριθμος που δίνουμε σε αυτή την παράγραφο θα αποτελούσε <
Θεωρούμε, ως συνήθως, το σύνολο κορυφών του γραφήματος να είναι το $[n]=\{1,2,\ldots,n\}$ και γράφουμε $w(i,j)$ για το βάρος της ακμής $(i,j)$ (το οποίο συμφωνούμε να θεωρούμε $+\infty$ αν η ακμή αυτή δεν υπάρχει).
Ο παρακάτω αλγόριθμος τροποποιεί σε κάθε επανάληψή του τον $n \times n$ πίνακα $A$ ο οποίος παίρνει αρχικές τιμές στο βήμα 1 και ενημερώνεται $n$ φορές στο βήμα 3. Με $w(i,j)$ συμβολίζουμε το βάρος της ακμής από το $i$ στο $j$. Αν δεν υπάρχει ακμή από το $i$ στο $j$ τότε θέτουμε $w(i, j)= +\infty$ ή έστω κάποια τεράστια (σε σχέση με το πρόβλημά μας) τιμή που η ύπαρξή της θα εξασφαλίσει ότι η (μη υπαρκτή) ακμή από το $i$ στο $j$ δε θα χρησιμοποιηθεί σε κανένα μονοπάτι μια και μας ενδιαφέρουν τα μονοπάτια μικρού μήκους.
Αλγόριθμος Floyd-Warshall
Θέτουμε $A^{(0)}_{ij} = w(i,j)$, για $i,j=1,\ldots,n$.
Επαναλαμβάνουμε για $k=1,2,\ldots,n$ το παρακάτω βήμα.
$A^{(k)}_{ij} = \min \{A^{(k-1)}_{ij},\ A^{(k-1)}_{ik}+A^{(k-1)}_{kj}\}$, για $i,j=1,\ldots,n$.
Θεώρημα Στο τέλος του προηγούμενου αλγορίθμου η απόσταση ανάμεσα στις κορυφές $i$ και $j$ είναι ίση με $A^{(n)}_{ij}$.
Απόδειξη: Θα δείξουμε με επαγωγή ως προς το $k$ ότι $A^{(k)}_{ij}$ ισούται με $L^{(k)}_{ij} = $ το μήκος του ελάχιστου μονοπατιού από το $i$ στο $j$ το οποίο όμως χρησιμοποιεί ενδιάμεσες κορυφές μόνο από το σύνολο $[k] = \{1,\ldots,k\}$.
Για $k=0$ το παραπάνω σύνολο είναι κενό και ο ισχυρισμός σημαίνει ότι $A^{(0)}_{ij}$ ισούται με το βάρος της πλευράς $(i,j)$ μια και το σύνολο των μονοπατιών από το $i$ στο $j$ που {\em δε} χρησιμοποιούν καμία ενδιάμεση κορυφή αποτελείται από την ακμή $(i,j)$ και μόνο. Άρα ο ισχυρισμός είναι αληθής για $k=0$.
Υποθέτουμε τώρα ότι ο ισχυρισμός ισχύει μέχρι και για $k-1$, θεωρούμε ένα ελάχιστο μονοπάτι από το $i$ στο $j$ που χρησιμοποιεί ενδιάμεσες κορυφές μόνο από το σύνολο $\{1,\ldots,k\}$, και ξεχωρίζουμε δύο περιπτώσεις.
(α) Το ελάχιστο αυτό μονοπάτι δε χρησιμοποιεί την κορυφή $k$.
(β) Χρησιμοποιεί την κορυφή $k$.
Στην πρώτη περίπτωση έχουμε φυσικά $L^{(k)}_{ij} = L^{(k-1)}_{ij}$.
Εστω ότι ισχύει το (β). Μπορούμε εύκολα να δείξουμε ότι όποιο και να είναι το ελάχιστο μονοπάτι από το $i$ στο $j$ περιέχει το $k$ ακριβώς μια φορά (αν το περιέχει δυο ή παραπάνω μπορούμε να το μικρύνουμε το μονοπάτι παραλείποντας ένα κομμάτι ανάμεσα σε δύο εμφανίσεις του $k$). Επίσης, το κομμάτι του μονοπατιού από το $i$ στο $k$ είναι ένα ελάχιστο μονοπάτι από το $i$ στο $k$ που χρησιμοποιεί ενδιάμεσες κορυφές από το σύνολο $\{1,\ldots,k-1\}$. Αρα το μήκος του είναι $L^{(k-1)}_{ik}$ και, ομοίως, το μήκος του μονοπατιού από το $k$ στο $j$ είναι $L^{(k-1)}_{kj}$. Το συνολικό μήκος του μονοπατιού είναι λοιπόν σ'αυτή την περίπτωση $$ L^{(k)}_{ij} = L^{(k-1)}_{ik} + L^{(k-1)}_{kj}. $$
Επίσης, σε κάθε περίπτωση, έχουμε τις ανισότητες $$ L^{(k)}_{ij} \le L^{(k-1)}_{ij} \ \ \text{και}\ \ L^{(k)}_{ij} \le L^{(k-1)}_{ik} + L^{(k-1)}_{kj}, $$ η πρώτη από τον ορισμό του του συμβόλου $L$ και μόνο και η δεύτερη παρατηρώντας ότι μπορούμε να πάμε από το $i$ στο $j$ (με ενδιάμεσους από το $[k]$) ακολουθώντας πρώτα ένα ελάχιστο μονοπάτι από το $i$ στο $k$ και μετά ένα ελάχιστο μονοπάτι από το $k$ στο $j$ (με ενδιάμεσους από το $[k-1]$).
Από τα παραπάνω προκύπτει ότι $$ L^{(k)}_{ij} = \min\{L^{(k-1)}_{ij}, L^{(k-1)}_{ik} + L^{(k-1)}_{kj}\} $$ και άρα, από τον τρόπο υπολογισμού των πινάκων $A^{(k)}$, έχουμε $A^{(k)}_{ij} = L^{(k)}_{ij}$, για κάθε $i,j=1,\ldots,n$, $k=0,\ldots,n$.
Υλοποίηση του αλγορίθμου
Πρέπει κατ' αρχην να δούμε πώς μπορούμε να αποθηκεύουμε και να επεξαργαζόμαστε διδιάστατους πίνακες με την Python. Ο απλούστερος τρόπος είναι ο εξής. Για να αποθηκεύσουμε ένα πίνακα $m \times n$ (με $m$ γραμμές δηλ. και $n$ στήλες) χρησιμοποιούμε μια λίστα που περιέχει $m$ στοιχεία (τις γραμμές του πίνακα). Κάθε στοιχείο αυτής της λίστας είναι μια λίστα που περιέχει $n$ στοιχεία, τα στοιχεία του πίνακα.
Αν θέλουμε π.χ. να αποθηκεύσουμε τον $2 \times 3$ πίνακα $$ M = \begin{array}{ccc} 3 & 3.1 & 2 \\ 1.5 & -3 & 3 \end{array} $$ μπορούμε να το κάνουμε ως εξής:
M = [ [3, 3.1, 2], [1.5, -3, 3] ]
Για να αναφερθούμε στο στοιχείο $M_{1,1}$ του πίνακα (η αρίθμησή μας από το 0 ως συνήθως) γράφουμε απλά M[1][1].
Πρώτη μας δουλειά λοιπόν είναι να μετατρέψουμε τα ονόματα των κορυφών μας από strings που είναι τώρα σε αριθμούς από 0 έως N-1, όπου N ο αριθμός όλων των κορυφών.
Το κάνουμε αυτό φτιάχνοντας δύο λεξικά (με N κλειδιά το καθένα). Το λεξικό number έχει ως κλειδιά τα ονόματα των πόλεων ως strings και ως τιμή κάθε πόλης είναι το όνομά της ως αριθμός από 0 έως N-1. Το λεξικό name κάνει ακριβώς την αντίστροφη δουλειά.
N = len(Graph.keys())
number = {} # Πρώτα υπολογίζουμε το λεξικό name
count = 0
for s in Graph.keys():
number[s] = count
count += 1
name = {} # και από το name υπολογίζουμε το λεξικό number
for s in number.keys():
name[number[s]] = s
print("Λεξικό name: ", name)
print("Λεξικό number: ", number)
Κατά τη διάρκεια του αλγορίθμου Floyd-Warshall θα χρειαστεί να υπολογίσουμε $N+1$ διαφορετικούς $N\times N$ πίνακες, τους
$$
A_{i,j}^{(k)},\ \ \text{ για } k=0, 1, \ldots, Ν.
$$
Κάθε ένας τέτοιος πίνακας $A^{(k)}$ χρειάζεται μόνο τον προηγούμενο πίνακα $A^{(k-1)}$ για να υπολογιστεί, οπότε δε χρειάζεται να τους αποθηκεύουμε όλους και αρκεί να κρατάμε κάθε φορά τον τελευταίο πίνακα που έχουμε υπολογίσει. Τον κρατάμε στη μεταβλητή A και υπολογίζουμε το νέο πίνακα (επόμενο $k$) στη μεταβλητή B. Έπειτα αντιγράφουμε τον πίνακα B στη μεταβλητή A και συνεχίζουμε έως ότου υπολογίσουμε τον τελευταίο πίνακα, ο οποίος αποτελεί και τη λύση στο πρόβλημά μας.
Αρχικοποιούμε τις μεταβλητές A και B παρακάτω. Η τιμή 1e6 (δηλ. $10^6$) που χρησιμοποιούμε για να γεμίσουμε αρχικά τον πίνακα A παίζει το ρόλο του $+\infty$. Σε θέσεις $i, j$ όπου υπάρχει ακμή στο γράφημα αυτή η τιμή αντικαθίσταται από το πραγματικό μήκος της ακμής.
A = []; B = []
row = N*[1e6] # Αυτή θα είναι μια γραμμή του πίνακα
for i in range(N): # Την αντιγράφουμε N φορές
A.append(row[:]) # προσοχή να δημιουργούμε νέο αντίγραφο κάθε φορά. αν γράφαμε row αντί για row[:] δε δουλεύει
B.append(row[:])
A[i][i] = 0 # τα στοιχεία της διαγωνίου είναι 0 αφού δεν κοστίζει τίποτα να πάμε από το i στο i
for s in Graph.keys(): # εδώ δίνουμε αρχικές τιμές στις θέσεις του πίνακα που αντιστοιχούν σε υπάρχουσες ακμές
for t in Graph[s].keys():
A[number[s]][number[t]] = Graph[s][t] # προσέξτε ότι χρησιμοποιούμε number[s] αντί για το όνομα s
Η επανάληψη είναι στο επόμενο.
for k in range(N):
for i in range(N):
for j in range(N):
B[i][j] = min(A[i][j], A[i][k]+A[k][j]) # αυτή είναι η βασική επανάληψη
for i in range(N): # εδώ αντιγράφουμε τον πίνακα B στον πίνακα A
for j in range(N):
A[i][j] = B[i][j]
Και εκτυπώνουμε τον πίνακα αποστάσεων παρακάτω.
for i in range(len(B)):
for j in range(len(B[0])):
print("{:4} ".format(B[i][j]), end='')
print()
Ποια είναι η απόσταση Χώρας Σφακίων ('ΧΣ') -- Μοίρες ('Μ');
B[number['ΧΣ']][number['Μ']]
Ακολουθεί ολόκληρο το πρόγραμμα στο επόμενο.
Graph = {
'ΧΣ': {'Χ': 60},
'Χ': {'ΧΣ': 60, 'Ρ': 60},
'Ρ': {'Χ': 60, 'Μ': 90, 'Η': 75},
'Μ': {'Ρ': 90, 'Η': 50},
'Η': {'Ρ': 75, 'Μ': 50, 'ΑΝ': 60},
'ΑΝ': {'Η': 60, 'ΠΑ': 20},
'ΠΑ': {'ΑΝ': 20, 'Ι': 20, 'Σ': 40},
'Ι': {'ΠΑ': 20},
'Σ': {'ΠΑ': 40},
}
N = len(Graph.keys())
number = {}
count = 0
for s in Graph.keys():
number[s] = count
count += 1
name = {}
for s in number.keys():
name[number[s]] = s
A = []; B = []
row = N*[1e6]
for i in range(N):
A.append(row[:])
B.append(row[:])
A[i][i] = 0
for s in Graph.keys():
for t in Graph[s].keys():
A[number[s]][number[t]] = Graph[s][t]
for k in range(N):
for i in range(N):
for j in range(N):
B[i][j] = min(A[i][j], A[i][k]+A[k][j])
for i in range(N):
for j in range(N):
A[i][j] = B[i][j]
for i in range(len(B)):
for j in range(len(B[0])):
print("{:4} ".format(B[i][j]), end='')
print()