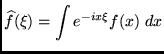
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ - ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ
Λεωφ. Κνωσού, 714 09 Ηράκλειο. Τηλ: +30 2810393800, Fax +30 2810393881

Σειρά Ομιλιών
Carleson's Theorem: Proof, Complements, Variations

Michael T. Lacey
Georgia Institute of Technology

Ιούλιος 2006, Αίθουσα θα ανακοινωθεί

Ο καθηγητής Lacey επισκέπτεται το Τμήμα Μαθηματικών στη «θέση Πηχωρίδη», τον Ιούλιο 2006. Θα δώσει σειρά ομιλιών με το ακόλουθο θέμα.

L. Carleson's celebrated theorem of 1965 asserts the pointwise convergence of the partial Fourier sums of square integrable functions. This Theorem, one of the three results pointed to in the recent Abel Prize citation for Carleson, is the main topic of these lectures. We give a proof of this fact, as it can be presented in brief self contained manner. We survey some of these variants, complements to Carleson's theorem, as well as open problems.

We are concerned with the Fourier transform on the real line, given by

$$\widehat f(\xi)=\int e^{-ix \xi} f(x)\;dx$$

for Schwartz functions $f$. For such functions, it is an important elementary fact that one has Fourier inversion,

$$f(x)=\lim_{N\to \infty}\frac1{2\pi}\int_{-N}^N \widehat f(\xi )e^{ix \xi}\; d \xi,\qquad x\in\mathbb{R},$$

the inversion holding for all Schwartz functions $f$. Indeed, the integral above is given by convolution with the Dirchlet kernel $D_N(x):=\frac{\sin Nx }{\pi x}$.

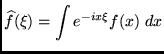
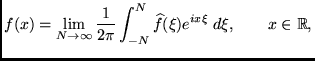
L. Carleson's theorem asserts that that the convergence holds almost everywhere, for $f\in L^2(\mathbb{R})$. The form of the Dirchlet kernel already points out the essential difficulties in establishing this theorem. That part of the kernel that is convolution with $\frac1 x$ corresponds to a singular integral. This can be done with the techniques associated to the Calderón Zygmund theory. In addition, one must establish some uniform control for the oscillatory term $\sin N x$, which falls outside of what is commonly considered to be part of the Calderón Zygmund theory.

The approach of the speaker and Christoph Thiele combines different elements to give a succinct proof of this fact. The first element is a combinatorial description of the Hilbert transform in a manner consistent with the symmetries of the Carleson operator. The group of elements consist of three Lemmas about this combinatorial model. A surprisingly easy Hilbertian argument; a variant of a classical covering lemma; and a particular $L^2$ estimate for the maximal function.

This proof is the foundation for what has grown into a rich theory of `modulation invariant Calderón Zygmund Theory.' We will survey some of these developments, including the bilinear Hilbert transform, and the Hilbert transform on vector fields. Connections to ergodic theory, and multilinear averages associated to Szemeredi's theorem are one possible direction of future developments.

http://fourier.math.uoc.gr/~ seminar