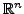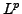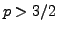The Hardy-Littlewood maximal function over a centrally symmetric convex body in $\mathbb{R}^n$ is known to be bounded on every $L^p$ for $p>3/2$ , with bounds independent of the dimension and the body (the case 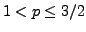$1<p\leq3/2$ is open). This is due to Bourgain and Carbery (independently). Their proofs are quite complicated and involve a substantial amount of "heavy" Fourier analysis. We will present a very short alternative proof which is based on different ideas (Calderón-Zygmund theory).