The main result of the Thesis is a lower bound for the maximal
possible number of facets of a 0/1 polytope in
![]() . By
definition, a 0/1 polytope is the convex hull of a subset of the
vertices of
. By
definition, a 0/1 polytope is the convex hull of a subset of the
vertices of ![]() .
.
In general, if ![]() is a polytope in
is a polytope in
![]() , we write
, we write
![]() for the number of its facets. Let
for the number of its facets. Let
![]() .
Fukuda and Ziegler asked what the behaviour of
.
Fukuda and Ziegler asked what the behaviour of ![]() is as
is as
![]() . The best known upper bound to date is
. The best known upper bound to date is
(for
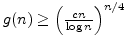 , where
, where
There exists a constantsuch that
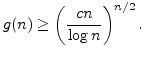
The existence of 0/1 polytopes with many facets is established
by a refinement of the probabilistic method developed by
Bárány and Pór. We work with ![]() polytopes (i.e.,
polytopes whose vertices are sequences of signs). Let
polytopes (i.e.,
polytopes whose vertices are sequences of signs). Let
![]() be independent and identically distributed
be independent and identically distributed ![]() random
variables, defined on some probability space
random
variables, defined on some probability space
![]() , with distribution
, with distribution
Set
There exist two positive constantsand
such that: for all sufficiently large
, and all
satisfying
, one has that
![$\displaystyle {\mathbb{E}}[f_{n-1}(K_N)]\geq \left (\frac{\log N}{a\log n}\right )^{n/2}.$](img29.png)
For the lower bound for ![]() one only has to choose
one only has to choose
![]() .
.
The second part of the Thesis is related to the strong form of
Sylvester's classical problem about random points uniformly
distributed in plane convex regions. We prove the following two
facts: (1) If ![]() is a plane convex body with area
is a plane convex body with area ![]() and if
and if
![]() denotes the distribution function of the area of a random
triangle in
denotes the distribution function of the area of a random
triangle in ![]() , then
, then
![]() for
all
for
all ![]() , where
, where ![]() is a triangle. If
is a triangle. If
![]() then
then ![]() is
a triangle. (2) If
is
a triangle. (2) If ![]() is a symmetric plane convex body with area
is a symmetric plane convex body with area
![]() and if
and if ![]() denotes the distribution function of the area
of a random symmetric parallelogram in
denotes the distribution function of the area
of a random symmetric parallelogram in ![]() , then
, then
![]() for all
for all ![]() , where
, where ![]() is a parallelogram. If
is a parallelogram. If
![]() then
then ![]() is a parallelogram.
is a parallelogram.