We show that a function 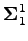$f$ on the unit circle has vanishing mean oscillation with respect to a non-atomic Borel measure $\mu$ if and only if it satisfies an asymptotic reverse Jensen inequality:

$$\lim_{\delta\to0}\sup_{\text{\textnormal{length}}(I)<\delta}\... ...t_Ie^fd\mu\right)\exp\left(-\frac1{\mu(I)}\int_Ifd\mu\right)=1.$$

This parallels the familiar fact that

$$\bigcup_{\lambda>0}e^{\lambda BMO}=A_\infty.$$

The "only if" part is a standard application of the John-Nirenberg inequality, whereas the "if" part requires different ideas. The higher dimensional case is open.