Suppose we put an 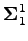 -disk around each lattice point in the plane, and then
we rotate this object around the origin for a set
-disk around each lattice point in the plane, and then
we rotate this object around the origin for a set  of angles.
When do we cover the whole plane, except for a neighborhood of the origin?
This is the problem we study in this paper.
It is very easy to see that if
of angles.
When do we cover the whole plane, except for a neighborhood of the origin?
This is the problem we study in this paper.
It is very easy to see that if
![$\Theta = [0,2\pi]$](img3.png) then we do indeed cover.
The problem becomes more interesting if we try to achieve covering with a small closed
set
then we do indeed cover.
The problem becomes more interesting if we try to achieve covering with a small closed
set  .
.
Joint work with Alex Iosevich and Máté Matolcsi.