Let
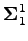 denote the space of all real polynomials of degree at most
denote the space of all real polynomials of degree at most  .
It is an old result of Stein and Wainger that
.
It is an old result of Stein and Wainger that
for some constant  depending only on
depending only on  . On the other hand, Carbery, Wainger and Wright claim that the true order of magnitude of the above principal value integral is
. On the other hand, Carbery, Wainger and Wright claim that the true order of magnitude of the above principal value integral is  . We prove that
. We prove that
![]() denote the space of all real polynomials of degree at most
denote the space of all real polynomials of degree at most ![]() .
It is an old result of Stein and Wainger that
.
It is an old result of Stein and Wainger that

