Θυμίζουμε ότι για ένα NFA η συνάρτηση μετάβασης ![]() είναι ο τρόπος
κωδικοποίησης των μεταβάσεων του.
Αν δηλ.
είναι ο τρόπος
κωδικοποίησης των μεταβάσεων του.
Αν δηλ. ![]() είναι μια κατάσταση και
είναι μια κατάσταση και
![]() είναι ένα
γράμμα του αλφαβήτου, το σύνολο
είναι ένα
γράμμα του αλφαβήτου, το σύνολο
![]() είναι το σύνολο όλων των καταστάσεων του NFA στις οποίες μπορεί αυτό
να μεταβεί όντας στην κατάσταση
είναι το σύνολο όλων των καταστάσεων του NFA στις οποίες μπορεί αυτό
να μεταβεί όντας στην κατάσταση ![]() και διαβάζοντας το γράμμα
και διαβάζοντας το γράμμα ![]() .
Αν στη θέση ενός ορίσματος της
.
Αν στη θέση ενός ορίσματος της ![]() μπει ολόκληρο σύνολο, τότε εννοούμε το σύνολο των εικόνων όταν το αντίστοιχο όρισμα
παίρνει τιμές μέσα σε αυτό το σύνολο:
μπει ολόκληρο σύνολο, τότε εννοούμε το σύνολο των εικόνων όταν το αντίστοιχο όρισμα
παίρνει τιμές μέσα σε αυτό το σύνολο:
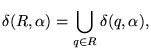
Επεκτείνουμε τώρα το πεδίο ορισμού της συνάρτησης ![]() όσον αφορά το δεύτερο όρισμά της.
Αν
όσον αφορά το δεύτερο όρισμά της.
Αν ![]() είναι μια κατάσταση και
είναι μια κατάσταση και
![]() είναι μια λέξη (ενδεχομένως και κενή) τότε ορίζουμε το σύνολο
καταστάσεων
είναι μια λέξη (ενδεχομένως και κενή) τότε ορίζουμε το σύνολο
καταστάσεων
![]() ως εξής:
ως εξής:
Με άλλα λόγια
![]() , είναι το σύνολο όλων εκείνων των καταστάσεων
του αυτομάτου στις οποίες μπορεί κανείς να βρεθεί ξεκινώντας από την κατάσταση
, είναι το σύνολο όλων εκείνων των καταστάσεων
του αυτομάτου στις οποίες μπορεί κανείς να βρεθεί ξεκινώντας από την κατάσταση ![]() και
ακολουθώντας τη λέξη
και
ακολουθώντας τη λέξη ![]() .
Και, αν
.
Και, αν
![]() είναι ένα σύνολο καταστάσεων, με
είναι ένα σύνολο καταστάσεων, με
![]() συμβολίζεται
το σύνολο όλων των καταστάσεων στις οποίες μπορεί κανείς να πάει ξεκινώντας
από κάποια κατάσταση στο
συμβολίζεται
το σύνολο όλων των καταστάσεων στις οποίες μπορεί κανείς να πάει ξεκινώντας
από κάποια κατάσταση στο ![]() και ακολουθώντας τη λέξη
και ακολουθώντας τη λέξη ![]() .
.
Παρατηρείστε τώρα ότι μια λέξη ![]() αναγνωρίζεται από ένα αυτόματο αν και μόνο αν
αναγνωρίζεται από ένα αυτόματο αν και μόνο αν
Είμαστε τώρα σε θέση να περιγράψουμε τον αλγόριθμο μετάβασης από ένα τυχόν
NFA ![]() σε ένα ισοδύναμο DFA
σε ένα ισοδύναμο DFA ![]() .
Έστω λοιπόν ότι το NFA
.
Έστω λοιπόν ότι το NFA ![]() είναι η πεντάδα
είναι η πεντάδα
![]() .
Το DFA
.
Το DFA
![]() θα έχει σύνολο καταστάσεων
θα έχει σύνολο καταστάσεων
![]() το δυναμοσύνολο (σύνολο όλων
των υποσυνόλων) του
το δυναμοσύνολο (σύνολο όλων
των υποσυνόλων) του ![]() ,
αρχική κατάσταση
,
αρχική κατάσταση
![]() , ίδιο αλφάβητο
, ίδιο αλφάβητο ![]() και τελικές
καταστάσεις όλα εκείνα τα σύνολα καταστάσεων του
και τελικές
καταστάσεις όλα εκείνα τα σύνολα καταστάσεων του ![]() που περιέχουν κάποια
τελική κατάσταση
που περιέχουν κάποια
τελική κατάσταση
Με λόγια τώρα: στο DFA ![]() που κατασκευάζουμε από την κατάσταση
που κατασκευάζουμε από την κατάσταση ![]() (υποσύνολο
του
(υποσύνολο
του ![]() ) με σύμβολο
) με σύμβολο
![]() μεταβαίνουμε στην κατάσταση
μεταβαίνουμε στην κατάσταση ![]() , που είναι
το σύνολο όλων εκείνων των καταστάσεων του
, που είναι
το σύνολο όλων εκείνων των καταστάσεων του ![]() στις οποίες μπορούμε να μεταβούμε
από κάποια κατάσταση του συνόλου
στις οποίες μπορούμε να μεταβούμε
από κάποια κατάσταση του συνόλου ![]() με
με ![]() κινούμενοι πάνω στο
κινούμενοι πάνω στο ![]() .
.
Ας δούμε τώρα πώς μετατρέπεται το ακόλουθο απλό NFA του Σχήματος 10 σε DFA. Το αποτέλεσμα δίνεται στο Σχήμα 11.
Το σύνολο καταστάσεων του ![]() θα είναι το δυναμοσύνολο του
θα είναι το δυναμοσύνολο του
![]() δηλ. το
δηλ. το
Δε θα δώσουμε εδώ την απλή επαγωγική (ως προς το μήκος της λέξης ![]() ) απόδειξη
του ότι η διαδικασία που περιγράψαμε παράγει ένα DFA
) απόδειξη
του ότι η διαδικασία που περιγράψαμε παράγει ένα DFA ![]() ισοδύναμο με το δοθέν
NFA
ισοδύναμο με το δοθέν
NFA ![]() , δηλ. τέτοιο ώστε η λέξη
, δηλ. τέτοιο ώστε η λέξη ![]() γίνεται αποδεκτή από το DFA
γίνεται αποδεκτή από το DFA ![]() αν και μόνο
αν γίνεται από το NFA
αν και μόνο
αν γίνεται από το NFA ![]() .
.
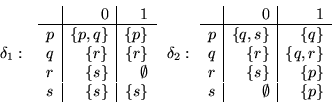
Μια ακόμη παραλλαγή του μοντέλου του πεπερασμένου αυτομάτου είναι το
μη ντετερμινιστικό αυτόματο με ![]() -κινήσεις.
Αυτό είναι ένα NFA που έχει, ενδεχομένως, και κάποιες ακμές που αντί να
έχουν ως ετικέτα ένα γράμμα του αλφαβήτου έχουν την κενή λέξη
-κινήσεις.
Αυτό είναι ένα NFA που έχει, ενδεχομένως, και κάποιες ακμές που αντί να
έχουν ως ετικέτα ένα γράμμα του αλφαβήτου έχουν την κενή λέξη ![]() .
Ας τα λέμε αυτά
.
Ας τα λέμε αυτά ![]() -NFA.
-NFA.
Το νόημα μιας ![]() -ακμής από μια κορυφή
-ακμής από μια κορυφή ![]() σε μια κορυφή
σε μια κορυφή ![]() είναι το εξής: αν το NFA βρίσκεται στην κατάσταση
είναι το εξής: αν το NFA βρίσκεται στην κατάσταση ![]() τότε μπορεί να επιλέξει
να μεταβεί στην κατάσταση
τότε μπορεί να επιλέξει
να μεταβεί στην κατάσταση ![]() χωρίς να διαβάσει το επόμενο
γράμμα της λέξης.
Το παρακάτω
χωρίς να διαβάσει το επόμενο
γράμμα της λέξης.
Το παρακάτω ![]() -NFA αναγνωρίζει τη γλώσσα
-NFA αναγνωρίζει τη γλώσσα ![]() , για παράδειγμα:
, για παράδειγμα:
Πώς αναγνωρίζει το αυτόματο του Σχήματος 12 τη λέξη
![]() ;
Κάνει δύο μεταβάσεις από την πρώτη κορυφή στον εαυτό της διαβάζοντας τα δύο 0, μετά μεταβαίνει
στη δεύτερη κορυφή χωρίς να διαβάσει τίποτα, μεταβαίνει από τη δεύτερη κορυφή στον
εαυτό της τρεις φορές διαβάζοντας τα 1, μεταβαίνει στην τρίτη κορυφή χωρίς
πάλι να διαβάσει τίποτα, και τέλος μεταβαίνει από την τρίτη κορυφή στον εαυτό της διαβάζοντας τα
πέντε 2.
;
Κάνει δύο μεταβάσεις από την πρώτη κορυφή στον εαυτό της διαβάζοντας τα δύο 0, μετά μεταβαίνει
στη δεύτερη κορυφή χωρίς να διαβάσει τίποτα, μεταβαίνει από τη δεύτερη κορυφή στον
εαυτό της τρεις φορές διαβάζοντας τα 1, μεταβαίνει στην τρίτη κορυφή χωρίς
πάλι να διαβάσει τίποτα, και τέλος μεταβαίνει από την τρίτη κορυφή στον εαυτό της διαβάζοντας τα
πέντε 2.
Αποδεικνύεται (αλλά παραλείπουμε την απόδειξη) ότι τα ![]() -NFA είναι ισοδύναμα
με τα NFA, και άρα και με τα DFA. Για κάθε
-NFA είναι ισοδύναμα
με τα NFA, και άρα και με τα DFA. Για κάθε ![]() -NFA δηλ. υπάρχει ένα NFA χωρίς
-NFA δηλ. υπάρχει ένα NFA χωρίς
![]() -κινήσεις που αναγνωρίζει την ίδια γλώσσα.
Για να μεταβούμε από ένα
-κινήσεις που αναγνωρίζει την ίδια γλώσσα.
Για να μεταβούμε από ένα ![]() -NFA
-NFA ![]() σε ένα ισοδύναμο NFA
σε ένα ισοδύναμο NFA ![]() κάνουμε τα εξής:
κάνουμε τα εξής: