

Next: 5.3 Τρ, 1/10/02: Σχέσεις,
Up: 5 Ημερολόγιο Μαθήματος (Διδακτικές
Previous: 5.1 Τρ, 24/9/02: Εισαγωγικά
Contents
Σήμερα κάναμε μια μικρή επανάληψη των εννοιών που είχαν
καλυφθεί στο προηγούμενο μάθημα.
Μιλήσαμε επίσης για δέντρα. Αυτά είναι μια πολύ ειδική και
σημαντική κατηγορία από κατευθυνόμενα γραφήματα.
Προκύπτει εύκολα από τα παραπάνω ότι κάθε κορυφή του δέντρου είναι
προσπελάσιμη με ακριβώς ένα μονοπάτι από τη ρίζα.
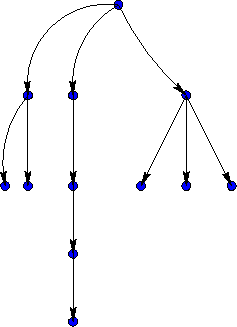
Ένα δέντρο απεικονίζεται στο παρακάτω σχήμα.
Σχήμα 2. Ένα δέντρο με 5 επίπεδα
Στη Θεωρία Γραφημάτων συναντάται συνήθως ο ορισμός του δέντρου
κάπως διαφορετικά: ένα μη κατευθυνόμενο γράφημα  λέγεται δέντρο
αν δεν έχει κύκλους, δεν έχει μονοπάτια δηλ. που ξεκινούν και τελειώνουν
στην ίδια κορυφή χωρίς να περνάνε πάνω από μια φορά από κάποια ακμή.
Αποδεικνύεται εύκολα ότι ο ορισμός αυτός συμπίπτει με αυτόν που δώσαμε
παραπάνω, αν κάποιος προσδιορίσει στο μη κατευθυνόμενο γράφημα το ποια
κορυφή θεωρείται ρίζα, και κατόπιν κατευθύνει όλες τις ακμές του γραφήματος
ώστε να ``απομακρύνονται'' από τη ρίζα.
λέγεται δέντρο
αν δεν έχει κύκλους, δεν έχει μονοπάτια δηλ. που ξεκινούν και τελειώνουν
στην ίδια κορυφή χωρίς να περνάνε πάνω από μια φορά από κάποια ακμή.
Αποδεικνύεται εύκολα ότι ο ορισμός αυτός συμπίπτει με αυτόν που δώσαμε
παραπάνω, αν κάποιος προσδιορίσει στο μη κατευθυνόμενο γράφημα το ποια
κορυφή θεωρείται ρίζα, και κατόπιν κατευθύνει όλες τις ακμές του γραφήματος
ώστε να ``απομακρύνονται'' από τη ρίζα.
Δείξαμε επίσης σήμερα το εξής:
Θεώρημα 1
Κάθε δέντρο με
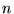
κορυφές έχει ακριβώς
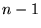
ακμές.
Δίνουμε δύο αποδείξεις παρακάτω, μια επαγωγική και μια όχι.
Η επαγωγική απόδειξη είναι τυπική της χρήσης της επαγωγής για
αποδείξεις στη Θεωρία Γραφημάτων.
Απόδειξη 1η:
Αυτή γίνεται με τη μέθοδο της επαγωγής ως πρός 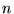 .
Η βασική περίπτωση είναι φυσικά η
.
Η βασική περίπτωση είναι φυσικά η 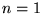 . Υπάρχει όμως μόνο
ένα δέντρο με μια κορυφή, και φυσικά αυτό δεν έχει καμιά
ακμή, αφού δεν υπάρχει άλλη κορυφή. Άρα το θεώρημα ισχύει σε αυτή
την περίπτωση.
. Υπάρχει όμως μόνο
ένα δέντρο με μια κορυφή, και φυσικά αυτό δεν έχει καμιά
ακμή, αφού δεν υπάρχει άλλη κορυφή. Άρα το θεώρημα ισχύει σε αυτή
την περίπτωση.
Αποδεικνύουμε τώρα το επαγωγικό βήμα. Υποθέτουμε δηλ. ότι
αν ένα δέντρο έχει το πολύ 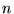 κορυφές τότε ισχύεει το θεώρημα και χρησιμοποιούμε
αυτή την υπόθεση για να δείξουμε την πρόταση για το τυχόν δέντρο με
κορυφές τότε ισχύεει το θεώρημα και χρησιμοποιούμε
αυτή την υπόθεση για να δείξουμε την πρόταση για το τυχόν δέντρο με 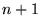 κορυφές. Έστω
κορυφές. Έστω 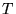 ένα τέτοιο δέντρο, και έστω
ένα τέτοιο δέντρο, και έστω
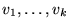 ,
, 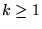 ,
οι απόγονοι της ρίζας. Με άλλα λόγια αυτές είναι οι κορυφές στο επίπεδο 1.
,
οι απόγονοι της ρίζας. Με άλλα λόγια αυτές είναι οι κορυφές στο επίπεδο 1.
Για κάθε
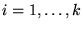 τώρα
παρατηρούμε τώρα ότι το γράφημα που προκύπτει από το
τώρα
παρατηρούμε τώρα ότι το γράφημα που προκύπτει από το 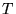 αν κρατήσουμε
μόνο τις κορυφές
αν κρατήσουμε
μόνο τις κορυφές 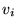 και τους απογόνους της είναι ένα δέντρο με ρίζα
την κορυφή
και τους απογόνους της είναι ένα δέντρο με ρίζα
την κορυφή 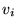 .
Αυτό το δέντρο, έστω
.
Αυτό το δέντρο, έστω 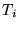 , ονομάζεται το υποδέντρο του
, ονομάζεται το υποδέντρο του 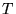 με ρίζα το
με ρίζα το 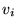 ,
και είναι φανερό ότι τα
,
και είναι φανερό ότι τα 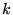 αυτά υποδέντρα είναι μεταξύ τους ξένα, δε
μοιράζονται δηλ. κορυφές ή ακμές.
αυτά υποδέντρα είναι μεταξύ τους ξένα, δε
μοιράζονται δηλ. κορυφές ή ακμές.
Αν με 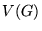 συμβολίζουμε το σύνολο των κορυφών του γραφήματος
συμβολίζουμε το σύνολο των κορυφών του γραφήματος 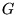 και
με
και
με 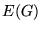 το σύνολο των ακμών του
το σύνολο των ακμών του 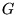 , αυτό που θέλουμε
να δείξουμε είναι
, αυτό που θέλουμε
να δείξουμε είναι
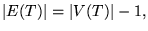 |
(1) |
όπου με
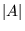 συμβολίζουμε τον πληθάριθμο του συνόλου
συμβολίζουμε τον πληθάριθμο του συνόλου 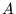 .
Η δε επαγωγική υπόθεση μας λέει ότι
.
Η δε επαγωγική υπόθεση μας λέει ότι
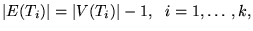 |
(2) |
μια και τα 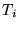 έχουν το πολύ
έχουν το πολύ 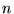 κορυφές.
κορυφές.
Ισχύουν όμως προφανώς (αφού τα 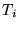 είναι ξένα μεταξύ τους)
είναι ξένα μεταξύ τους)
Αντικαθιστώντας στην (1)
και χρησιμοποιώντας τις σχέσεις (2)
προκύπτει ισότητα.

Απόδειξη 2η:
Το σύνολο των ακμών μπορεί να έρθει σε αμφιμονοσήμαντη αντιστοιχία
με το σύνολο των κορυφών πλην της ρίζας, αντιστοιχίζοντας σε κάθε
ακμή 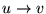 την κορυφή
την κορυφή 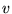 . Η απεικόνιση αυτή είναι 1-1 και επί αφού ακριβώς
μια ακμή καταλήγει σε κάθε κορυφή πλην της ρίζας.
Άρα τα δύο αυτά σύνολα είναι ισοπληθικά, δηλ. το πλήθος των ακμών
είναι ίσο με αυτό των κορυφών πλην ένα.
. Η απεικόνιση αυτή είναι 1-1 και επί αφού ακριβώς
μια ακμή καταλήγει σε κάθε κορυφή πλην της ρίζας.
Άρα τα δύο αυτά σύνολα είναι ισοπληθικά, δηλ. το πλήθος των ακμών
είναι ίσο με αυτό των κορυφών πλην ένα.

Άσκηση 5.2.1
Δείξτε ότι οι κορυφές ενός δέντρου μπορούν να χρωματιστούν με δύο
χρώματα ώστε δύο κορυφές που συνδέονται με μια ακμή αναγκαστικά να έχουν
διαφορετιό χρώμα.
Άσκηση 5.2.2
Σε ένα δέντρο υπάρχει το πολύ ένα μονοπάτι που
ενώνει δύο δεδομένες κορυφές.
Άσκηση 5.2.3
Άν ένα δέντρο έχει το πολύ
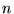
επίπεδα και από κάθε κορυφή ξεκινούν το πολύ 5
ακμές, πόσες το πολύ κορυφές έχει το δέντρο;



Next: 5.3 Τρ, 1/10/02: Σχέσεις,
Up: 5 Ημερολόγιο Μαθήματος (Διδακτικές
Previous: 5.1 Τρ, 24/9/02: Εισαγωγικά
Contents
Mihalis Kolountzakis
2003-09-04
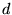 που ονομάζεται το βάθος του δέντρου.
που ονομάζεται το βάθος του δέντρου.
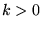 βρίσκονται ακριβώς τα παιδιά των κορυφών του
επιπέδου
βρίσκονται ακριβώς τα παιδιά των κορυφών του
επιπέδου 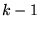 , όλες δηλ. εκείνες οι κορυφές
, όλες δηλ. εκείνες οι κορυφές 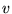 για τις οποίες
υπάρχει μια κορυφή
για τις οποίες
υπάρχει μια κορυφή 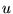 στο επίπεδο
στο επίπεδο 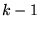 τ.ώ. υπάρχει η ακμή
τ.ώ. υπάρχει η ακμή 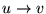 .
.
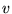 εκτός τη ρίζα έχει ακριβώς ένα γονέα, δηλ.
μια κορυφή
εκτός τη ρίζα έχει ακριβώς ένα γονέα, δηλ.
μια κορυφή 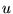 τ.ώ.
τ.ώ. 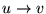 . Η ρίζα δεν έχει κανένα.
. Η ρίζα δεν έχει κανένα.