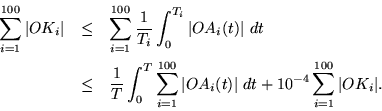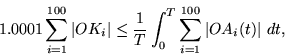Next: 3 Πρόβλημα 2 (2/7/2001) Up: Προβλήματα για το Μαθηματικό Previous: 1 Γιατί υπάρχει αυτή Contents

2001)

Το παρακάτω πρόβλημα ήταν ένα από αυτά που ρωτήθηκαν πέρυσι. Το (α) έχει μια πολύ απλή λύση, ενώ για να λυθεί το (β) πρέπει να έχει κανείς κατανοήσει καλά κάποιες έννοιες της Ανάλυσης.

Πρόβλημα 1 (α) Πάνω σε ένα τραπέζι βρίσκονται τοποθετημένα 100 ρολόγια. Τα ρολόγια έχουν όλα την ίδια περίοδο, είναι στρογγυλά με λεπτοδείκτη, μπορούν όμως να είναι τοποθετημένα πάνω στο τραπέζι με οποιοδήποτε τρόπο. Επίσης οι διάμετροι των ρολογιών μπορούν να είναι διαφορετικές. Δείξτε ότι κάποια χρονική στιγμή το άθροισμα των αποστάσεων του κέντρου Ο του τραπεζιού από τα κέντρα των ρολογιών θα είναι μικρότερο ή ίσο από το άθροισμα των αποστάσεων του Ο από τα άκρα των λεπτοδεικτών.
(β) Αν παραλείψουμε την υπόθεση ότι τα ρολόγια έχουν όλα την ίδια περίοδο, δείξτε ότι κάποια χρονική στιγμή το άθροισμα των αποστάσεων του Ο από τα άκρα των λεπτοδεικτών θα είναι μεγαλύτερο ή ίσο από 0.9 φορές το άθροισμα των αποστάσεων του Ο από τα κέντρα των ρολογιών.

Υπόδειξη για το (α) (28/6/2001): Αν είστε άτυχοι τώρα ξαναπεράστε μετά από μισή ώρα.

Μία λύση για το πρόβλημα (1/7/2001) (Αγησίλαος και Μανούσος-Γαβριήλ Αθανασούλης)

Ακολουθεί η λύση που προτείνω εγώ, η οποία είναι αρκετά διαφορετική από την αμέσως προηγούμενη. Προσέξτε ότι αποφεύγεται οποιαδήποτε εξέταση του αν οι περίοδοι είναι μεταξύ τους σύμμετρες ποσότητες (έχουν ρητό λόγο δηλαδή) ή όχι. Το επιχείρημα του μέσου όρου (αν ο μέσος όρος κάποιων ποσοτήτων είναι μεγαλύτερος από τότε κάποια από τις ποσότητες αυτές είναι μεγαλύτερη από ) παίζει κεντρικό ρόλο και στις δύο λύσεις.

(α) Έστω , $i=1,\ldots,100$ , οι θέσεις των λεπτοδεικτών μια χρονική στιγμή , και έστω οι αντίστοιχες θέσεις μετά από μισή ώρα, όπου η περίοδος των ρολογιών θεωρείται πως είναι μια ώρα. Έστω επίσης τα κέντρα των ρολογιών. Έχουμε τότε

$\begin{displaymath} OK_i = {1\over 2}(OA_i+OB_i), (i=1,\ldots,100). \end{displaymath}$

Χρησιμοποιώντας την τριγωνική ανισότητα και προσθέτοντας για όλα τα

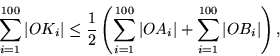
$\begin{displaymath} \sum_{i=1}^{100} {\left\vert{OK_i}\right\vert} \le {1\over2}... ...ert} + \sum_{i=1}^{100} {\left\vert{OB_i}\right\vert} \right), \end{displaymath}$

άρα ένα από τα δύο αθροίσματα δεξιά οφείλει να είναι μεγαλύτερο ή ίσο από την ποσότητα αριστερά, που είναι αυτό που θέλουμε.

(β) Έστω οι περίοδοι των ρολογιών (όλα τα είναι ίσα με στο (α)) και πάρτε ένα τεράστιο συγκριτικά με όλα τα . Έστω επίσης η θέση του -οστού λεπτοδείκτη τη χρονική στιγμή . Έχουμε

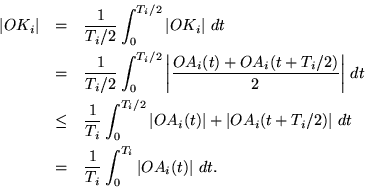
$\begin{eqnarray*} {\left\vert{OK_i}\right\vert} &=& {1\over T_i/2}\int_0^{T_i/2}... ...=& {1\over T_i}\int_0^{T_i} {\left\vert{OA_i(t)}\right\vert} dt. \end{eqnarray*}$

Εύκολα βλέπει κανείς (αξίζει να δουλέψετε αυτή τη λεπτομέρεια μόνοι σας) ότι παίρνοντας το

αρκετά μεγάλο σε σχέση με τα

μπορούμε να πετύχουμε οι δύο μέσοι όροι

$\begin{displaymath} {1\over T_i}\int_0^{T_i} {\left\vert{OA_i(t)}\right\vert} dt... ... } {1\over T}\int_0^{T} {\left\vert{OA_i(t)}\right\vert} dt \end{displaymath}$

να διαφέρουν ο ένας από τον άλλο λιγότερο από

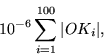
$\begin{displaymath} 10^{-6}\sum_{i=1}^{100} {\left\vert{OK_i}\right\vert}, \end{displaymath}$

η οποιαδήποτε άλλη ποσότητα προδιαγράψουμε - πρώτα λέμε από τι θέλουμε να φράσσεται η διαφορά των δύο μέσων όρων και μετά χρησιμοποιούμε αυτή τη συνθήκη για να προσδιορίσουμε το

Προσθέτοντας τώρα για όλα τα την ανισότητα που αποδείξαμε πιο πάνω παίρνουμε

$\begin{eqnarray*} \sum_{i=1}^{100} {\left\vert{OK_i}\right\vert} &\le& \sum_{i=... ...t} dt + 10^{-4} \sum_{i=1}^{100} {\left\vert{OK_i}\right\vert}. \end{eqnarray*}$

’ρα

$\begin{displaymath} 1.0001 \sum_{i=1}^{100} {\left\vert{OK_i}\right\vert} \le ... ...\int_0^T \sum_{i=1}^{100} {\left\vert{OA_i(t)}\right\vert} dt, \end{displaymath}$

οπότε για κάποια χρονική στιγμή, αφού το ολοκλήρωμα δεξιά είναι ο μέσος όρος του αθροίσματος $\sum_{i=1}^{100} {\left\vert{OA_i(t)}\right\vert}$ , το άθροισμα αυτό θα είναι μεγαλύτερο ή ίσο από το αριστερό μέλος, που είναι τουλάχιστον τόσο καλό όσο αυτό που θέλαμε να δείξουμε.

Mihalis Kolountzakis