Next: 5 Πρόβλημα 4 (15/7/2001) Up: Προβλήματα για το Μαθηματικό Previous: 3 Πρόβλημα 2 (2/7/2001) Contents

2001)

Δίδεται πραγματική ολοκληρώσιμη συνάρτηση 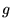ορισμένη στο 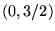. Υποθέτουμε ότι

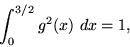$\begin{displaymath} \int_0^{3/2} g^2(x) dx = 1, \end{displaymath}$

(1)

και

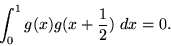$\begin{displaymath} \int_0^1 g(x) g(x+{1\over2}) dx = 0. \end{displaymath}$

(2)

Δείξτε ότι

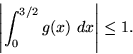$\begin{displaymath} {\left\vert{\int_0^{3/2} g(x) dx}\right\vert} \le 1. \end{displaymath}$

(3)

Λύση (Φάνης Ματσούκας - fffanis@yahoo.com)

Γράφουμε

$\begin{displaymath} g_0(x) = g(x), g_1(x) = g(x+1/2), g_2(x) = g(x+1) (x\in(0,1/2)), \end{displaymath}$

αλλιώς ορίζουμε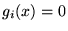

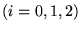. Έχουμε τότε

$\begin{displaymath} g(x) = g_0(x) + g_1(x-1/2) + g_2(x-1), (x\in(0,3/2)). \end{displaymath}$

(Οι συναρτήσεις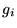

``ζούν'' μέσα στο

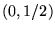Ο παρακάτω συμβολισμός (εσωτερικό γινόμενο) είναι και κλασικός και απλουστεύει πολύ τα παρακάτω, οπότε τον εισάγουμε:

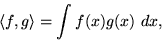$\begin{displaymath} {\langle f, g \rangle} = \int f(x)g(x) dx, \end{displaymath}$

(4)

όπου ο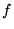ι

και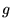

είναι δυο ολοκληρώσιμες πραγματικές συναρτήσεις και το ολοκλήρωμα εκτείνεται στο κοινό πεδίο ορισμού τους (αλλιώς, τις επεκτείνουμε με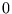

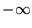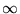εκτός του πεδίου ορισμού και ολοκληρώνουμε από $-\infty$ έως $\infty$ ).

Θυμίζουμε επίσης της κλασική ανισότητα Cauchy-Schwartz

$\begin{displaymath} {\left\vert{{\langle f, g \rangle}}\right\vert}^2 \le {\langle f, f \rangle}\cdot{\langle g, g \rangle}. \end{displaymath}$

Η σχέση (1) γράφεται τώρα

$\begin{displaymath} {\langle g_0, g_0 \rangle}+{\langle g_1, g_1 \rangle}+{\langle g_2, g_2 \rangle} = 1. \end{displaymath}$

Επίσης η (2) γράφεται μετά από μια απλή αντικατάσταση

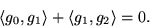$\begin{displaymath} {\langle g_0, g_1 \rangle} + {\langle g_1, g_2 \rangle} = 0. \end{displaymath}$

(5)

Αυτό που θέλουμε να δείξουμε, μετά από τετραγωνισμό, είναι

$\begin{displaymath} {\left\vert{\int g_0+g_1+g_2}\right\vert}^2 \le 1. \end{displaymath}$

Χρησιμοποιώντας την ανισότητα Cauchy-Schwartz για τις συναρτήσεις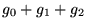

και τη χαρακτηριστική συνάρτηση του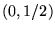

, παίρνουμε

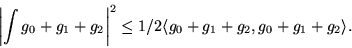$\begin{displaymath} {\left\vert{\int g_0+g_1+g_2}\right\vert}^2 \le 1/2 {\langle g_0+g_1+g_2, g_0+g_1+g_2 \rangle}. \end{displaymath}$

(6)

Αρκεί δηλ. να δείξουμε ότι

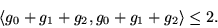$\begin{displaymath} {\langle g_0+g_1+g_2, g_0+g_1+g_2 \rangle} \le 2. \end{displaymath}$

(7)

Εφαρμόζοντας την επιμεριστική ιδιότητα του εσωτερικού γινομένου το αριστερό μέρος αυτής γίνεται, μετά από χρήση της (5)

$\begin{displaymath} {\langle g_0, g_0 \rangle}+{\langle g_1, g_1 \rangle}+{\langle g_2, g_2 \rangle} + 2{\langle g_0, g_2 \rangle}, \end{displaymath}$

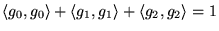οπότε, επειδή ισχύει η ${\langle g_0, g_0 \rangle}+{\langle g_1, g_1 \rangle}+{\langle g_2, g_2 \rangle}=1$ , για να δειχτεί η (7) πρέπει και αρκεί να δειχτεί

$\begin{displaymath} {\left\vert{{\langle g_0, g_2 \rangle}}\right\vert} \le 1/2. \end{displaymath}$

Χρησιμοποιώντας πάλι την Cauchy-Schwartz παίρνουμε

$\begin{displaymath} {\left\vert{{\langle g_0, g_2 \rangle}}\right\vert}^2 \le {\langle g_0, g_0 \rangle} {\langle g_2, g_2 \rangle}. \end{displaymath}$

Επειδή

$\begin{displaymath} {\langle g_0, g_0 \rangle} + {\langle g_2, g_2 \rangle} \le 1 \end{displaymath}$

έπεται όμως ότι

$\begin{displaymath} {\langle g_0, g_0 \rangle} \cdot {\langle g_2, g_2 \rangle} \le 1/4 \end{displaymath}$

(ανισότητα αριθμητικού-γεωμετρικού μέσου) πού είναι ακριβώς αυτό που θέλουμε να δείξουμε.

Next: 5 Πρόβλημα 4 (15/7/2001) Up: Προβλήματα για το Μαθηματικό Previous: 3 Πρόβλημα 2 (2/7/2001) Contents

Mihalis Kolountzakis