5.7 Τρ, 22/10/02: Κλειστότητα κανονικών γλωσσών κάτω από απλές πράξεις. Το Λήμμα άντλησης.

5.7.1 Κλειστότητα κανονικών γλωσσών

Από τον ορισμό των κανονικών εκφράσεων και των γλωσσών είναι φανερό ότι αν $L_1$ και $L_2$ είναι κανονικές γλώσσες τότε κανονική είναι και η $L_1 \cup L_2$ όπως και η γλώσσα $L_1^*$. Δεν είναι καθόλου προφανές από τον ορισμό των κανονικών εκφράσεων το αν η γλώσσα

$$L_1^c = {\left\{{w \in \Sigma^*:  w \notin L_1}\right\}}$$

είναι κανονική. Γίνεται όμως και αυτό φανερό αν χρησιμοποιήσουμε το βασικό αποτέλεσμα που λέει ότι μια γλώσσα είναι κανονική αν και μόνο αν υπάρχει ένα DFA που την αναγνωρίζει. Έστω λοιπόν ότι το DFA $M$ αναγνωρίζει τη γλώσσα $L_1$. Φτιάνχουμε ένα DFA $M'$ από το $M$ κρατώντας τις ίδιες καταστάσεις, αλφάβητο, αρχική κατάσταση και ακμές του $M$ αλλά κάνουμε όλες τις τελικές καταστάσεις του $M$ μη τελικές και όλες τις μη τελικές καταστάσεις του $M$ τις κάνουμε τελικές στο $M'$. (Εδώ πρέπει να είμαστε λίγο προσεκτικοί και να δουλεύουμε στο μορφή του $M$ που δε χρησιμοποιεί συντομογραφία, αλλά που ικανοποιεί την αρχική απαίτηση για DFA, ότι δηλ. για κάθε κατάσταση και για κάθε γράμμα του αλφαβήτου υπάρχει ακριβώς μια ακμή.) Είναι φανερό τώρα ότι μια λέξη γίνεται δεκτή στο $M'$ αν και μόνο αν δε γίνεται δεκτή στο $M$, άρα το $M'$ είναι ένα DFA για τη γλώσσα $L_1^c$.

Είναι τώρα εύκολο να δείξουμε ότι και η γλώσσα $L_1 \cap L_2$ είναι κανονική. Αρκεί να δείξουμε ότι το συμπλήρωμά της είναι, αλλά

$$(L_1 \cap L_2)^c = L_1^c \cup L_2^c,$$

και από αυτά που είπαμε προηγουμένως προκύπτει ο ισχυρισμός.

Ορισμός 4   Αντικατάσταση (substitution) σε ένα αλφάβητο $\Sigma$ είναι μια οποιαδήποτε αντιστοίχιση των γραμμάτων του αλφαβήτου σε γλώσσες πάνω από το $\Sigma$, μια οποιαδήποτε συνάρτηση δηλ.

$$f: \Sigma \to 2^{\Sigma^*},$$

μια συνάρτηση δηλ. που παίρνει τιμές τυχόντα υποσύνολα του $\Sigma^*$. Αν για κάθε $\alpha\in\Sigma$ η γλώσσα $f(a)$ είναι κανονική, τότε και η αντικατάσταση ονομάζεται κανονική.

Έχοντας μια αντικατάσταση $f: \Sigma \to 2^{\Sigma^*}$ μπορούμε να επεκτείνουμε το πεδίο ορισμού της από γράμματα του $\Sigma$ σε λέξεις του $\Sigma^*$. Αν $w = \alpha_1 \cdots \alpha_n$, $\alpha_i \in \Sigma$, είναι μια λέξη, τότε ορίζουμε (χρησιμοποιούμε το ίδιο σύμβολο $f$ για να συμβολίσουμε και την επεκτεταμένη συνάρτηση)

$$f(w) = f(\alpha_1)\cdots f(\alpha_n),$$

η γλώσσα δηλ. που προκύπτει από τη συγκόλληση των γλωσσών $f(\alpha_1),\ldots,f(\alpha_n)$.

Αν $L$ είναι μια γλώσσα ορίζουμε ως συνήθως

$$f(L) = \bigcup_{w \in L} f(w).$$

Θεώρημα 3   Αν $L$ κανονική, και η αντικατάσταση $f$ είναι κανονική, τότε η $f(L)$ είναι κανονική γλώσσα.

Σκίτσο απόδειξης. Αφού η $L$ είναι κανονική τότε προκύπτει ως γλώσσα μιας κανονικής έκφρασης $r$. Είναι εύκολο να δούμε (αλλά δεν το κάνουμε με λεπτομέρεια εδώ) ότι η γλώσσα $f(L)$ είναι ακριβώς αυτή που προκύπτει αν τροποποιήσουμε την έκφραση $r$ αντικαθιστώντας κάθε γράμμα $\alpha$ που εμφανίζεται στην $r$ με μια κανονική έκφραση για τη γλώσσα $f(\alpha)$. Άρα η γλώσσα $f(L)$ δίδεται από κανονική έκφραση, άρα είναι κανονική.
$\Box$

Ορισμός 5   Μια αντικατάσταση $f$ λέγεται ομομορφισμός αν για κάθε $\alpha\in\Sigma$ γλώσσα $f(\alpha)$ είναι μονοσύνολο.

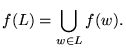
Επειδή κάθε πεπερασμένο σύνολο λέξεων είναι κανονική γλώσσα (γιατί;) από το προηγούμενο θεώρημα έπεται ότι οι ομομορφισμοί διατηρούν την κανονικότητα των γλωσσών.

Ορισμός 6   Αν $f$ είναι ομομορφισμός και $L$ είναι μια γλώσσα, η αντίστροφη ομομορφική εικόνα της $L$ είναι η γλώσσα

$$f^{-1}(L) = {\left\{{w\in\Sigma^*:   f(w) \in L}\right\}}.$$

Θεώρημα 4   Αν $f$ ομομορφισμός και $L$ κανονική γλώσσα τότε και η $f^{-1}(L)$ είναι κανονική.

Απόδειξη. Έστω $M$ ένα DFA που αναγνωρίζει την $L$. Φτιαχνουμε DFA $M'$ ως εξής: κρατάμε ίδιες καταστασεις και αρχικές και τελικές καταστάσεις με το $M$ και ορίζουμε μόνο νέα συνάρτηση μετάβασης ως εξής: αν $q$ είναι μια κατάσταση του $M$ και $\alpha\in\Sigma$ ορίζουμε

$$\delta_{M'}(q, \alpha) = \delta_M(q, f(\alpha)).$$

Μεταβαίνουμε δηλ. στο $M'$ σε εκείνη την κατάσταση όπου θα καταλήγαμε αν στο $M$ ξεκινάγαμε από την κατάσταση $q$ και ακολουθούσαμε τη λέξη $f(\alpha)$. Είναι φανερό ότι η λέξη $w$ γίνεται αποδεκτή από το $M'$ αν και μόνο αν η λέξη $f(w)$ γίνεται αποδεκτή από το $M$, άρα το DFA αναγνωρίζει τη γλώσσα $f^{-1}(L)$, οπότε αυτή είναι κανονική.
$\Box$

Άσκηση 5.7.1   Αν $L$ είναι κανονική γλώσσα τότε και η γλώσσα

$$L^R = {\left\{{x \in \Sigma^*:   x^R \in L}\right\}}$$

είναι κανονική. Με $x^R$ συμβολίζουμε τη λέξη $x$ με τα γράμματά της σε ανάποδη σειρά. Π.χ. $011^R = 110$.

5.7.2 Το Λήμμα Άντλησης (Pumping lemma) και μη κανονικές γλώσσες

Υπάρχουν γλώσσες που δεν είναι κανονικές. Αυτό είναι προφανές για πολύ γενικούς λόγους, που δεν έχουν τόσο πολύ να κάνουν με τη φύση των κανονικών γλωσσών, παρά μόνο με το γεγονός ότι κάθε κανονική γλώσσα επιδέχεται μια πεπερασμένη περιγραφή. Αυτή μπορεί να είναι είτε μια κανονική έκφραση, είτε η δομή ενός DFA που την αναγνωρίζει, για παράδειγμα.

Πόσες όμως διαφορετικές πεπερασμένες περιγραφές υπάρχουν;

Είναι φανερό ότι αυτές είνάι άπειρες το πλήθος (αφού π.χ. υπάρχουν οσοδήποτε μεγάλες κανονικές εκφράσεις), αλλά αυτό δεν είναι επαρκής πληροφορία για το πλήθος τους. Είναι πολύ πιο ακριβές το ότι υπάρχουν αριθμήσιμες το πλήθος πεπερασμένες περιγραφές, μπορούν δηλ. όλες οι πεπερασμένες περιγραφές να απαριθμηθούν: η περιγραφή 1, η περιγραφή 2, ..., η περιγραφή Ν, ..., με τρόπο ώστε να μη μείνει καμιά περιγραφή απ' έξω. Αυτός είναι ο ορισμός ενός αριθμήσιμου συνόλου. Ένα σύνολο δηλ. λέγεται αριθμήσιμο αν υπάρχει μια 1-1 απεικόνιση του συνόλου αυτού στους φυσικούς αριθμούς (βεβαιωθείτε ότι το καταλαβαίνετε αυτό).

Το γιατί το σύνολο όλων των πεπερασμένων εκφράσεων (πάνω από ένα σταθερό αλφάβητο $\Sigma$) είναι αριθμήσιμο είναι απλό. Αφού το $\Sigma$ είναι πεπερασμένο υπάρχουν πεπερασμένο το πλήθος εκφράσεις που μπορούν να φτιάξουμε με μήκος $n$, για κάθε $n$. Για την ακρίβεια, υπάρχουν το πολύ ${\left\vert{\Sigma}\right\vert}^n$ τέτοιες εκφράσεις. Για να απαριθμήσουμε λοιπόν το σύνολο όλων των πεπερασμένων εκφράσεων, αριθμούμε πρώτα τις εκφράσεις μήκους 1, μετά αυτές μήκους 2, και συνεχίζουμε κατ' αυτόν τον τρόπο, ώστε δε μένει τίποτα αμέτρητο.

Είναι αρκετά πιο δύσκολο (και παραλείπουμε την απόδειξη) να δούμε ότι το σύνολο όλων των υποσυνόλων οποιουδήποτε άπειρου συνόλου δεν είναι αριθμήσιμο. Έτσι, το σύνολο όλων των γλωσσών πάνω από το $\Sigma$, δηλ. το σύνολο όλων των υποσυνόλων του άπειρου συνόλου $\Sigma^*$ δεν είναι αριθμήσιμο. Άρα υπάρχει κάποια γλώσσα που δεν έχει αντίστοιχη πεπερασμένη περιγραφή, οπότε δεν είναι κανονική.

Το παραπάνω είναι ένα πολύ γενικό επιχείρημα, όπως είπαμε, και δεν εξαρτάται σχεδόν καθόλου από το τι εννοούμε κανονική γλώσσα, παρά μόνο ότι, ό,τι κι αν εννοούμε, η κανονική γλώσσα μπορεί να περιγραφεί πλήρως με μια πεπερασμένη ακολουθία από γράμματα, διαλεγμένα από ένα πεπερασμένο αλφάβητο. Με τον ίδιο τρόπο φαίνεται, π.χ. ότι υπάρχουν συναρτήσεις $f:{\mathbf N}\to{\mathbf N}$ που δεν είναι υπολογίσιμες από πρόγραμμα, ουσιαστικά ότι κι αν εννούμε με αυτό. Ας πούμε για παράδειγμα ότι θεωρούμε μια τέτοια συνάρτηση υπολογίσιμη αν υπάρχει ένα πρόγραμμα σε κάποια γλώσσα προγραμματισμού, ας πούμε την C που υπολογίζει τη συνάρτηση αυτή. Μα ένα πρόγραμμα αποτελεί πεπερασμένη περιγραφή της συνάρτησης, άρα, επειδή το πλήθος των συναρτήσεων $f:{\mathbf N}\to{\mathbf N}$ δεν είναι αριθμήσιμο, υπάρχει κάποια στην οποία δεν αντιστοιχεί πρόγραμμα, που δεν είναι δηλ. υπολογίσιμη.

Δε βοηθάει όμως αυτό το επιχείρημα στο να αποδείξει κανείς ότι συγκεκριμένες γλώσσες δεν είναι κανονικές. Αν και γνωρίζουμε δηλ. ότι οι περισσότερες γλώσσες (υπό μία έννοια) δεν είναι κανονικές, είναι παρ' όλα αυτά δύσκολο να δείξουμε αυτό για μια συγκεκριμένη γλώσσα που μας δίδεται, π.χ. για την

$$L_1 = {\left\{{0^n1^n:   n=0,1,2,\ldots}\right\}}.$$

Αυτή η γλώσσα απαρτίζεται από όλες τις λέξεις που έχουν αρχικά μια ομάδα από μηδενικά και μετά μια ίση σε μήκος ομάδα από άσσους, και τίποτε άλλο. Θα δούμε σε λίγο ένα τρόπο απόδειξης του ότι η $L_1$ δεν είναι κανονική. Διαισθητικά όμως ο λόγος είναι ο εξής (το παρακάτω δεν αποτελεί απόδειξη): ένα αυτόματο είναι ουσιαστικά ισοδύναμο με ένα υπολογιστή σαν κι αυτούς που ξέρουμε με μόνο τον περιορισμό ότι ο υπολογιστής αυτός έχει πεπερασμένη και σταθερή μνήμη, δεν εξαρτάται δηλ. η ποσότητα της μνήμης του από το πρόβλημα που έχει να λύσει. Αν είχαμε ένα πρόγραμμα που τρέχει σε ένα τέτοιο υπολογιστή και το οποίο αναγνωρίζει τη γλώσσα $L_1$, αυτό το πρόγραμμα θα είχε πρόσβαση σε μνήμη της οποίας το μήκος δε μπορεί να εξαρτάται από το μήκος της λέξης προς αναγνώριση. Όμως, δε μπορούμε να φανταστούμε ένα πρόγραμμα (αλγόριθμο) που θα αποφασίζει αν μια λέξη ανήκει στην $L_1$ ή οχι χωρίς να ``θυμάται'' κάπου το πόσα μηδενικά έχει δει. Κι αυτό δε γίνεται αν ο αριθμός των μηδενικών είνάι πολύ μεγάλος, γιατί όσο αυξάνει το πλήθος των μηδενικών τόσο αυξάνει, χωρίς άνω φράγμα, το πλήθος των ψηφίων (η μνήμη) που χρειαζόμαστε για να αποθηκεύσουμε τον αριθμό αυτό.

Είναι δύσκολο να μετατρέψουμε το παραπάνω διαισθητικό επιχείρημα σε απόδειξη, οπότε η μέθοδος που ακολουθούμε για να δείξουμ εότι η $L_1$ δενείναι κανονική είναι αρκετά διαφορετική. Χρησιμοποιούμε το ακόλουθο πολύ χρήσιμο λήμμα.

Θεώρημα 5 (Λήμμα Άντλησης - Pumping Lemma)  
Έστω ότι η $L$ είναι κανονική. Τότε υπάρχει φυσικός αριθμός $n$ (ο οποίος δε χρειάζεται να είναι μεγαλύτερος από τον ελάχιστο αριθμό καταστάσεων ενός DFA που αναγνωρίζει την $L$) ώστε για κάθε λέξη $z \in L$ με ${\left\vert{z}\right\vert} \ge n$, μπορούμε να γράψουμε

$$z = uvw, (u,v,w \in \Sigma^*, {\left\vert{v}\right\vert}\ge 1, {\left\vert{uv}\right\vert} \le n),$$

ούτως ώστε για κάθε $i=0,1,2,\ldots$, η λέξη $uv^iw \in L$ (αυτή είναι η λέξη που αρχίζει με $u$ ακολουθείται από την $v$ οποιοδήποτε πεπερασμένο αριθμό από φορές - ακόμη και 0-και τελειώνει με $w$).

Απόδειξη: Έστω $M$ ένα DFA με ελάχιστο αριθμό καταστάσεων που αναγνωρίζει τη γλώσσα $L$, και έστω $n$ το πλήθος των καταστάσεων του $M$. Αν η λέξη $z$ αναγνωρίζεται τότε ξεκινώντας από την αρχική κορυφή $q_0$ καταλήγουμε διαβάζοντας την $z$, με ${\left\vert{z}\right\vert} = m \ge n$, σε κάποια τελική κορυφή $q_1$ διανύοντας ένα μονοπάτι πάνω στο $M$:

$$q_0 = q_{i_1} \to q_{i_2} \to \cdots \to q_{i_{m+1}} = q_1$$

όπου το πλήθος των ακμών είναι $m$ (μια ακμή για κάθε γράμμα της $z$) και άρα το πλήθος των κορυφών είναι $m+1 > n$. Συμπεραίνουμε ότι υπάρχουν κάποιες κορυφές που εμφανίζονται τουλάχιστον δύο φορές στο μονοπάτι. Από αυτές τις κορυφές ονομάζουμε $q$ αυτή που πρωτοεμφανίζεται για δεύτερη φορά στο μονοπάτι και ονομάζουμε $v$ τη λέξη που μεσολαβεί μέχρι την επόμενη εμφάνιση της $q$, ενώ $u$ ονομάζομε το πρόθεμα της $z$ μέχρι την πρώτη εμφάνιση της $q$ και $w$ ονομάζομε το επίθεμα της $z$ μετά τη δεύτερη εμφάνιση της $q$ (βλ. Σχήμα 17).

Σχήμα 17. Το μονοπάτι που αντιστοιχεί στη λέξη $uvw$

Είναι φανερό ότι ${\left\vert{v}\right\vert}\ge 1$ και ότι ${\left\vert{uv}\right\vert}\le n$, αφού σίγουρα όταν θα έχουμε διαβάσει το $n$-οστό γράμμα της $z$ θα έχουμε ήδη δεί τουλάχιστον μια κορυφή δύο φορές, και ανάμεσα σε αυτές που έχουμε δεί δύο φορές η πρώτη είναι εξ ορισμού η $q$. Επίσης είναι φανερό ότι το βρόγχο που ξεκινά και τελειώνει στην $q$ μπορούμε να μην το διανύσουμε καθόλου (οπότε δείχνουμε ότι η λέξη $uw \in L$) ή να τον διανύσουμε όσες φορές θέλουμε, ας πούμε $i$. Άρα η λέξη $uv^iw \in L$, όπως οφείλαμε να δείξουμε.
$\Box$

Πώς χρησιμοποιούμε το Λήμμα Άντλησης για να δείξουμε ότι η γλώσσα $L_1$ δεν είναι κανονική; Υποθέτουμε ότι είναι και καταλήγουμε σε άτοπο. Αν είναι λοιπόν, υπάρχει, από το Λήμμα Άντλησης, ένας φυσικός αριθμός $n$, τέτοις ώστε αν $z\in L_1$ και ${\left\vert{z}\right\vert} \ge n$ τότε ισχύουν τα συμπεράσματα του Λήμματος. Έχουμε $z = 0^n1^n \in L_1$ και ${\left\vert{z}\right\vert} \ge n$, άρα $z = uvw$, με ${\left\vert{uv}\right\vert}\le n$ και μη κενό $v$, τέτοια ώστε για κάθε $i=0,1,\ldots$ έχουμε $uv^iw \in L_1$. Αυτό όμως δε γίνεται μια και η λέξη $uv^2w=uvvw$ έχει σίγουρα περισσότερα 0 απ' ότι 1, αφού, λόγω του ότι ${\left\vert{uv}\right\vert}\le n$, και το $u$ και το $v$ έχουν μόνο μηδενικά μέσα τους.

Ας δούμε τώρα άλλη μια εφαρμογή του λήμματος άντλησης σε παρόμοιο πρόβλημα. Για κάθε λέξη $x=\alpha_1\cdots\alpha_n$, $\alpha_i \in \Sigma$, ορίζουμε την αντεστραμμένη λέξη $x^R = \alpha_n \cdots \alpha_1$, να είναι η $x$ με αντεστραμμένη τη σειρά των γραμμάτων του. Ορίζουμε τη γλώσσα

$$L_2 = {\left\{{x\in (0+1)^*:    x = x^R}\right\}},$$

να απαρτίζεται από όλες εκείνες τις λέξεις που διαβάζονται το ίδιο από αριστερά και από τα δεξιά.

Δείχνουμε τώρα ότι η $L_2$ δεν είναι κανονική. Έστω ότι είναι και έστω $n$ ο φυσικός αριθμός του οποίου η ύπαρξη προκύπτει από το Λήμμα Άντλησης. Ορίζουμε τη λέξη $z = 1^n01^n$ που είναι στην $L_2$. Γράφεται τότε η $z$ ως $z = uvw$, με μη κενό $v$ και ${\left\vert{uv}\right\vert}\le n$, οπότε και οι λέξεις $u$, $v$ έχουν μέσα μόνο 1, ώστε $uv^iw \in L_2$, για $i=0,1,2,\ldots$. Αλλά προφανώς η λέξη $uw \notin L_2$ αφού αφαιρώντας το $v$ αφαιρέσαμε κάποιους άσσους από την αριστερή ομάδα άσσων αλλά όχι από τη δεξιά ομάδα, οπότε έχουμε καταλήξει σε άτοπο, άρα η $L_2$ δεν είναι κανονική.

Άσκηση 5.7.2   Ποιες από τις παρακάτω γλώσσες του $(0+1)^*$ είναι κανονικές;

1. ${\left\{{0^{2n}:   n\ge 1}\right\}}$
2. ${\left\{{0^m1^n0^{m+n}:   m,n\ge 1}\right\}}$
3. Οι λέξεις που δεν έχουν τρία διαδοχικά μηδενικά
4. Λέξεις με τόσα μηδενικά όσα και άσσους.
5. ${\left\{{xwx^R:    x,w \in (0+1)^+}\right\}}$