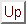
Next: 9 Πρόβλημα 8 (17/9/01) Up: Προβλήματα για το Μαθηματικό Previous: 7 Πρόβλημα 6 (14/8/2001) Contents

2001)

(Όπως ήταν διατυπωμένο το πρόβλημα δεν ίσχυε για μικρές τιμές του .)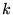

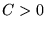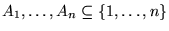Δείξτε ότι υπάρχει μια σταθερά τέτοια ώστε οποτεδήποτε έχουμε σύνολα $A_1, \ldots, A_n \subseteq {\left\{{1,\ldots,n}\right\}}$ ώστε η τομή δύο οποιωνδήποτε από αυτά έχει το πολύ 10 στοιχεία να ισχύει

$\begin{displaymath} \sum_{i=1}^n {\left\vert{A_i}\right\vert} \le C n^{3/2}. \end{displaymath}$

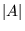( ${\left\vert{A}\right\vert}$ συμβολίζει τον πληθάριθμο του συνόλου

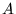Υπόδειξη: Ορίζουμε τις χαρακτηριστικές συναρτήσεις

$\begin{displaymath} \chi_i(j) = \left\{\begin{array}{ll} 1 & j\in A_i\\ 0 & j\notin A_i. \end{array}\right. \end{displaymath}$

και γράφουμε τώρα 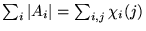$\sum_i{\left\vert{A_i}\right\vert} = \sum_{i,j} \chi_i(j)$ . Η άσκηση λύνεται με έξυπνη χρήση της ανισότητας Cauchy-Schwartz και της υπόθεσης.

Λύση από τον Τ. Ζαντορόζνι

Mihalis Kolountzakis